
【题目】已知![]() (n∈N*)的展开式中第五项的系数的与第三项的系数的比是10∶1.
(n∈N*)的展开式中第五项的系数的与第三项的系数的比是10∶1.
(1)求展开式中各项系数的和;
(2)求展开式中含![]() 的项;
的项;
(3)求展开式中系数最大的项和二项式系数最大的项.
【答案】(1)1;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)已知![]() 的展开式中第五项系数与第三项的系数的比是
的展开式中第五项系数与第三项的系数的比是![]() ,由此关系建立起方程,求出
,由此关系建立起方程,求出![]() ;(2)由(1)
;(2)由(1)![]() ,利用展开式中项的公式
,利用展开式中项的公式![]() ,令
,令![]() 的指数为
的指数为![]() 解出
解出![]() ,即可得到
,即可得到![]() 的项;(3)利用
的项;(3)利用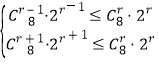 ,得出展开式中系数最大的项 .
,得出展开式中系数最大的项 .
解:由题意知,第五项系数为C·(-2)4,第三项的系数为C·(-2)2,则![]() ,
,
化简得n2-5n-24=0,
解得n=8或n=-3(舍去).
(1)令x=1得各项系数的和为(1-2)8=1.
(2)通项公式Tr+1=C (![]() )8-r
)8-r![]() =C (-2)rx
=C (-2)rx![]() -2r,
-2r,
令![]() -2r=
-2r=![]() ,则r=1.
,则r=1.
故展开式中含![]() 的项为
的项为![]() .
.
(3)设展开式中的第r项,第r+1项,第r+2项的系数绝对值分别为C![]() ·2r-1,C·2r,C
·2r-1,C·2r,C![]() ·2r+1,
·2r+1,
若第r+1项的系数绝对值最大,
则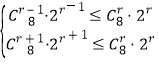 解得5≤r≤6.
解得5≤r≤6.
又T6的系数为负,所以系数最大的项为T7=1 792x-11
由n=8知第5项二项式系数最大,
此时![]() .
.


 出彩同步大试卷系列答案
出彩同步大试卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)是定义域为R上的奇函数,当x>0时,f(x)=x2+2x.
(1)求f(x)的解析式;
(2)若不等式f(t﹣2)+f(2t+1)>0成立,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校进行课题实验,乙班为实验班,甲班为对比班,甲乙两班均有50人,一年后对两班进行测试,成绩如下表
甲班成绩 |
|
|
|
|
|
人数 | 4 | 20 | 15 | 10 | 1 |
乙班成绩 |
|
|
|
|
|
人数 | 1 | 11 | 23 | 13 | 2 |
(1)现从甲班成绩位于![]() 内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果
内的试卷中抽取9份进行试卷分析,请问用什么抽样方法更合理,并写出最后的抽样结果
(2)完成下列![]() 列联表,并判断有多大把握认为这两个班在这次测试中成绩的差异与实施课题实验有关。
列联表,并判断有多大把握认为这两个班在这次测试中成绩的差异与实施课题实验有关。
成绩小于100 | 成绩不小于100 | 合计 | |
甲班 | 50 | ||
乙班 | 50 | ||
合计 | 36 | 64 | 100 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】运货卡车以每小时x千米的速度匀速行驶130千米,按交通法规限制50≤x≤100(单位:千米/时).假设汽油的价格是每升2元,而汽车每小时耗油![]() 升,司机的工资是每小时14元.
升,司机的工资是每小时14元.
(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某快递公司收取快递费用的标准是:重量不超过![]() 的包裹收费
的包裹收费![]() 元;重量超过
元;重量超过![]() 的包裹,除
的包裹,除![]() 收费
收费![]() 元之外,超过
元之外,超过![]() 的部分,每超出
的部分,每超出![]() (不足
(不足![]() ,按
,按![]() 计算)需再收
计算)需再收![]() 元.该公司将最近承揽的
元.该公司将最近承揽的![]() 件包裹的重量统计如下:
件包裹的重量统计如下:
包裹重量(单位: |
|
|
|
|
|
包裹件数 |
|
|
|
|
|
公司对近![]() 天,每天揽件数量统计如下表:
天,每天揽件数量统计如下表:
包裹件数范围 |
|
|
|
|
|
包裹件数 (近似处理) |
|
|
|
|
|
天数 |
|
|
|
|
|
以上数据已做近似处理,并将频率视为概率.
(1)计算该公司未来![]() 天内恰有
天内恰有![]() 天揽件数在
天揽件数在![]() 之间的概率;
之间的概率;
(2)(i)估计该公司对每件包裹收取的快递费的平均值;
(ii)公司将快递费的三分之一作为前台工作人员的工资和公司利润,剩余的用作其他费用.目前前台有工作人员![]() 人,每人每天揽件不超过
人,每人每天揽件不超过![]() 件,工资
件,工资![]() 元.公司正在考虑是否将前台工作人员裁减
元.公司正在考虑是否将前台工作人员裁减![]() 人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润更有利?
人,试计算裁员前后公司每日利润的数学期望,并判断裁员是否对提高公司利润更有利?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,点
,点![]() 在椭圆C上.
在椭圆C上.
(1)求椭圆C的方程;
(2)设动直线![]() 与椭圆C有且仅有一个公共点,判断是否存在以原点O为圆心的圆,满足此圆与
与椭圆C有且仅有一个公共点,判断是否存在以原点O为圆心的圆,满足此圆与![]() 相交两点
相交两点![]() ,
,![]() (两点均不在坐标轴上),且使得直线
(两点均不在坐标轴上),且使得直线![]() ,
,![]() 的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
的斜率之积为定值?若存在,求此圆的方程;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com