
曲线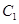 的参数方程为
的参数方程为 (
( 为参数),将曲线
为参数),将曲线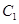 上所有点的横坐标伸长为原来的2倍,纵坐标伸长为原来的
上所有点的横坐标伸长为原来的2倍,纵坐标伸长为原来的 倍,得到曲线
倍,得到曲线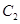 .
.
(Ⅰ)求曲线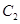 的普通方程;
的普通方程;
(Ⅱ)已知点 ,曲线
,曲线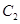 与
与 轴负半轴交于点
轴负半轴交于点 ,
, 为曲线
为曲线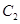 上任意一点, 求
上任意一点, 求 的最大值.
的最大值.
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:解答题
在极坐标系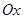 中,直线
中,直线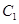 的极坐标方程为
的极坐标方程为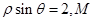 是
是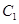 上任意一点,点P在射线OM上,且满足
上任意一点,点P在射线OM上,且满足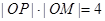 ,记点P的轨迹为
,记点P的轨迹为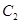 。
。
(Ⅰ)求曲线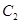 的极坐标方程;
的极坐标方程;
(Ⅱ)求曲线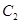 上的点到直线
上的点到直线 距离的最大值。
距离的最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
以原点 为极点,以
为极点,以 轴的正半轴为极轴建立极坐标系,已知曲线
轴的正半轴为极轴建立极坐标系,已知曲线 ,过点
,过点 的直线
的直线 的参数方程为
的参数方程为 ,设直线
,设直线 与曲线
与曲线 分别交于
分别交于 ;
;
(1)写出曲线 和直线
和直线 的普通方程;
的普通方程;
(2)若 成等比数列,求
成等比数列,求 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(1) 在直角坐标系xOy中,曲线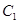 的参数方程为
的参数方程为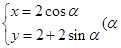 为参数),M为
为参数),M为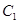 上的动点,P点满足
上的动点,P点满足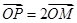 ,点P的轨迹为曲线
,点P的轨迹为曲线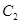 .已知在以O为极点,x轴的正半轴为极轴的极坐标系中,射线
.已知在以O为极点,x轴的正半轴为极轴的极坐标系中,射线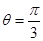 与
与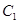 的异于极点的交点为A,与
的异于极点的交点为A,与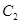 的异于极点的交点为B,求|AB|.
的异于极点的交点为B,求|AB|.
(2) 某旅游景点给游人准备了这样一个游戏,他制作了“迷尼游戏板”:在一块倾斜放置的矩形胶合板上钉着一个形如“等腰三角形”的八行铁钉,钉子之间留有空隙作为通道,自上而下第1行2个铁钉之间有1个空隙,第2行3个铁钉之间有2个空隙,…,第8行9个铁钉之间有8个空隙(如图所示).东方庄家的游戏规则是:游人在迷尼板上方口放人一球,每玩一次(放入一球就算玩一次)先付给庄家2元.若小球到达①②③④号球槽,分别奖4元、2元、0元、-2元.(一个玻璃球的滚动方式:通过第1行的空隙向下滚动,小球碰到第二行居中的铁钉后以相等的概率滚入第2行的左空隙或右空隙.以后小球按类似方式继续往下滚动,落入第8行的某一个空隙后,最后掉入迷尼板下方的相应球槽内).恰逢周末,某同学看了一个小时,留心数了数,有80人次玩.试用你学过的知识分析,这一小时内游戏庄家是赢是赔? 通过计算,你得到什么启示?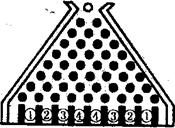
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
本题有(1)、(2)、(3)三个选答题,每小题7分,请考生任选2个小题作答,满分14分.如果多做,则按所做的前两题记分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.
(1)(本小题满分7分)选修4—2:矩阵与变换
在平面直角坐标系 中,把矩阵
中,把矩阵 确定的压缩变换
确定的压缩变换 与矩阵
与矩阵 确定的旋转变换
确定的旋转变换 进行复合,得到复合变换
进行复合,得到复合变换 .
.
(Ⅰ)求复合变换 的坐标变换公式;
的坐标变换公式;
(Ⅱ)求圆
 在复合变换
在复合变换 的作用下所得曲线
的作用下所得曲线 的方程.
的方程.
(2)(本小题满分7分)选修4-4:坐标系与参数方程
在平面直角坐标系 中,直线
中,直线 的参数方程为
的参数方程为 (
(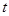 为参数),
为参数), 、
、 分别为直线
分别为直线 与
与 轴、
轴、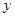 轴的交点,线段
轴的交点,线段 的中点为
的中点为 .
.
(Ⅰ)求直线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)以坐标原点 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,求点
轴的正半轴为极轴建立极坐标系,求点 的极坐标和直线
的极坐标和直线 的极坐标方程.
的极坐标方程.
(3)(本小题满分7分)选修4—5:不等式选讲
已知不等式 的解集与关于
的解集与关于 的不等式
的不等式 的解集相等.
的解集相等.
(Ⅰ)求实数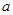 ,
, 的值;
的值;
(Ⅱ)求函数 的最大值,以及取得最大值时
的最大值,以及取得最大值时 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知曲线C的极坐标方程是 ,以极点为平面直角坐标系的原点,极轴为X轴的正半轴,建立平面直角坐标系,直线
,以极点为平面直角坐标系的原点,极轴为X轴的正半轴,建立平面直角坐标系,直线 的参数方程是:
的参数方程是: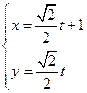 ,求直线
,求直线 与曲线C相交所称的弦的弦长。
与曲线C相交所称的弦的弦长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com