解:(I)证明:∵a
1=1,S
n=na
n-2n(n-1),
S
n+1=(n+1)a
n+1-2(n+1)n,
∴a
n+1=S
n+1-S
n=(n+1)a
n+1-na
n-4n,
∴a
n+1-a
n=4,
∴数列{a
n}是首项为1,公差为4的等差数列,
∴a
n=1+(n-1)•4=4n-3.
(II)由(I)知:a
n=4n-3,
∴
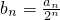
=
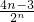
,
∴
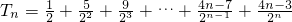
,
∴
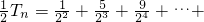
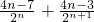
,
两式相减,得:

+…+

)-
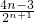
=
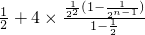
-
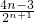
=
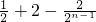
-
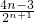
,
∴
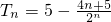
.
(III)∵
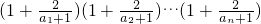
≥
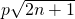
对一切n∈N
*均成立,
即
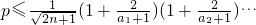
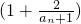
对一切n∈N
*均成立,
只需p≤
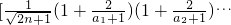
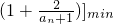 min
min,n∈N
*,
令
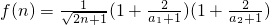
…
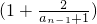
,n≥2,且n∈N
*,
则
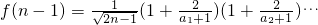
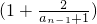
,n≥2,且n∈N
*,

=
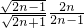
=
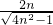
>1,n≥2,且n∈N
*,
∴f(n)>f(n-1),n≥2,且n∈N
*,
即f(n)在n∈N
*上为增函数,
∴
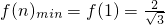
=

,
∴
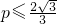
,
故实数p的最大值是

.
分析:(I)由a
1=1,S
n=na
n-2n(n-1),知S
n+1=(n+1)a
n+1-2(n+1)n,故a
n+1=S
n+1-S
n=(n+1)a
n+1-na
n-4n,所以a
n+1-a
n=4,由此能求出数列{a
n}的通项公式.
(II)由a
n=4n-3,知
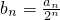
=
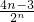
,所以
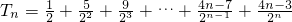
,由错位相减法能求出
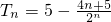
.
(III)由
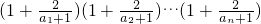
≥
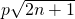
对一切n∈N
*均成立,知
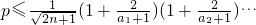
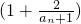
对一切n∈N
*均成立,只需p≤
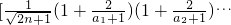
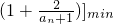 min
min,n∈N
*,由此能求出实数p的最大值.
点评:本题考查数列与不等式的综合应用,考查运算求解能力,推理论证能力;考查化归与转化思想.对数学思维的要求比较高,有一定的探索性.综合性强,难度大,易错点是求使不等式
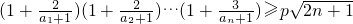
对一切n∈N
*均成立的等价命题的转化,是高考的重点.解题时要认真审题,仔细解答.

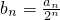 ,求数列{bn}的前n项和Tn;
,求数列{bn}的前n项和Tn;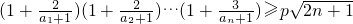 对一切n∈N*均成立的最大实数p的值.
对一切n∈N*均成立的最大实数p的值.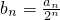 =
=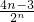 ,
,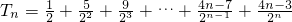 ,
,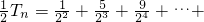
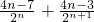 ,
, +…+
+…+ )-
)-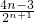
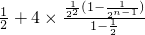 -
-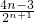
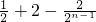 -
-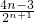 ,
,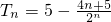 .
.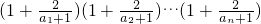 ≥
≥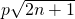 对一切n∈N*均成立,
对一切n∈N*均成立,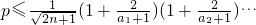
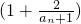 对一切n∈N*均成立,
对一切n∈N*均成立,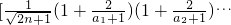
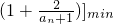 min,n∈N*,
min,n∈N*,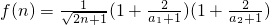 …
…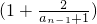 ,n≥2,且n∈N*,
,n≥2,且n∈N*,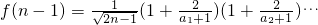
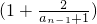 ,n≥2,且n∈N*,
,n≥2,且n∈N*, =
=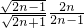 =
=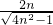 >1,n≥2,且n∈N*,
>1,n≥2,且n∈N*,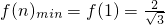 =
= ,
,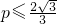 ,
, .
.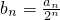 =
=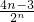 ,所以
,所以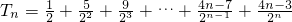 ,由错位相减法能求出
,由错位相减法能求出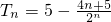 .
.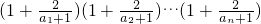 ≥
≥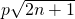 对一切n∈N*均成立,知
对一切n∈N*均成立,知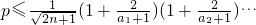
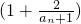 对一切n∈N*均成立,只需p≤
对一切n∈N*均成立,只需p≤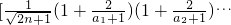
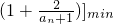 min,n∈N*,由此能求出实数p的最大值.
min,n∈N*,由此能求出实数p的最大值.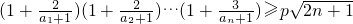 对一切n∈N*均成立的等价命题的转化,是高考的重点.解题时要认真审题,仔细解答.
对一切n∈N*均成立的等价命题的转化,是高考的重点.解题时要认真审题,仔细解答. 

 阅读快车系列答案
阅读快车系列答案