
| A. | [$\frac{5}{4}$,$\frac{7}{4}$] | B. | [0,$\frac{7}{4}$] | C. | [$\frac{5}{4}$,$\frac{7}{3}$] | D. | [1,$\frac{7}{3}$] |
分析 判断函数f(x)的奇偶性和单调性,将不等式进行转化,利用直线和圆的位置关系,结合数形结合和$\frac{y}{x+1}$的几何意义即可得到结论.
解答 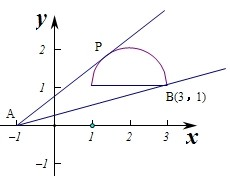 解:∵f(x)=x+sinx(x∈R),
解:∵f(x)=x+sinx(x∈R),
∴f(-x)=-x-sinx=-(x+sinx)=-f(x),
即f(x)=x+sinx(x∈R)是奇函数.
∵f(y2-2y+3)+f(x2-4x+1)≤0,
∴f(y2-2y+3)≤-f(x2-4x+1)=f[-(x2-4x+1)],
由f′(x)=1+cosx≥0,∴函数单调递增.
∴(y2-2y+3)≤-(x2-4x+1),
即(y2-2y+3)+(x2-4x+1)≤0,
∴(y-1)2+(x-2)2≤1,∵当y≥1时,$\frac{x+y+1}{x+1}$=1+$\frac{y-0}{x+1}$,
∴不等式对应的平面区域为圆心为(2,1),半径为1的圆的上半部分.
而$\frac{y}{x+1}$的几何意义为动点P(x,y)到定点A(-1,0)的斜率的取值范围.
设k=$\frac{y}{x+1}$,(k>0),则y=kx+k,即kx-y+k=0.
当直线和圆相切时,圆心到直线的距离d=$\frac{|2k-1+k|}{\sqrt{{1+k}^{2}}}$=$\frac{|3k-1|}{\sqrt{{1+k}^{2}}}$=1
即8k2-6k=0,解得k=$\frac{3}{4}$.此时直线斜率最大.
当直线kx-y+k=0经过点B(3,1)时,直线斜率最小,
此时3k-1+k=0,即4k=1,解得k=$\frac{1}{4}$,
∴$\frac{1}{4}$≤k≤$\frac{3}{4}$,故 $\frac{x+y+1}{x+1}$=1+$\frac{y-0}{x+1}$=1+k的取值范围是[$\frac{5}{4}$,$\frac{7}{4}$].
故选:A
点评 本题主要考查直线和圆的位置关系的应用,函数奇偶性和单调性的判断以及直线斜率的取值范围,综合性较强,运算量较大,利用数形结合是解决本题的基本思想,属于中档题.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{4}{5}$ | B. | $-\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | .1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在△ABC中,角A、B、C所对的边分别为a、b、c,满足a=2sinA,cosC=-$\frac{1}{2}$
在△ABC中,角A、B、C所对的边分别为a、b、c,满足a=2sinA,cosC=-$\frac{1}{2}$查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com