
分析 (1)通过设正项等差数列{an}的公差为d,并利用首项和公差d表示出a2、a6,通过a1+3,2a2+2,a6+8成等比数列构造方程,进而计算可得结论;
(2)通过(1)可知$\frac{1}{{a}_{{2}^{n-1}}}$=$\frac{1}{{2}^{n}}$,利用等比数列的求和公式计算可知Pn=1-$\frac{1}{{2}^{n}}$,通过裂项可知$\frac{1}{{S}_{n}}$=$\frac{1}{n}$-$\frac{1}{n+1}$,进而并项相加即得结论.
解答 (1)解:设正项等差数列{an}的公差为d,则d≥0,
依题意,a2=2+d,a6=2+5d,
∵a1+3,2a2+2,a6+8成等比数列,
∴(6+2d)2=(2+3)(10+5d),
整理得:36+24d+4d2=50+25d,即4d2-d-14=0,
解得:d=2或d=-$\frac{7}{4}$(舍),
∴数列{an}的通项公式an=2n;
(2)证明:由(1)可知$\frac{1}{{a}_{{2}^{n-1}}}$=$\frac{1}{2×{2}^{n-1}}$=$\frac{1}{{2}^{n}}$,
由等比数列的求和公式可知Pn=$\frac{1}{{a}_{1}}$+$\frac{1}{{a}_{2}}$+$\frac{1}{{a}_{4}}$+…+$\frac{1}{{a}_{{2}^{n-1}}}$=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$=1-$\frac{1}{{2}^{n}}$,
∵$\frac{1}{{S}_{n}}$=$\frac{1}{2×\frac{n(n+1)}{2}}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
∴Qn=$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+$\frac{1}{{S}_{3}}$+…+$\frac{1}{{S}_{n}}$
=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+…+$\frac{1}{n}$-$\frac{1}{n+1}$
=1-$\frac{1}{n+1}$,
显然,当n≥1时$\frac{1}{n+1}$≥$\frac{1}{{2}^{n}}$,故Pn≥Qn.
点评 本题考查数列的通项及前n项和,考查裂项相消法,注意解题方法的积累,属于中档题.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
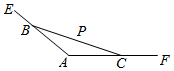 如图,已知tan∠EAF=-2,点P到AE、AF的距离分别为$\sqrt{5}$,3,过P点的直线BC与AE,AF分别交于B,C两点,则△ABC的面积的最小值为15.
如图,已知tan∠EAF=-2,点P到AE、AF的距离分别为$\sqrt{5}$,3,过P点的直线BC与AE,AF分别交于B,C两点,则△ABC的面积的最小值为15.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$x±y=0 | B. | x±$\sqrt{3}$y=0 | C. | x±$\sqrt{2}$y=0 | D. | $\sqrt{3}$x±y=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9h | B. | 10h | C. | 11h | D. | 12h |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com