
分析 (1)利用排列数公式能求出数字1,2,3,4,5能组成多少个没有重复数字的五位数.
(2)先求出数字1,2,3,4,5能组成没有重复数字的五位数的个数,再求出其中能被5整除的数字的个数,由此利用等可能事件概率计算公式能求出所得的五位数中任取一个,那么所得数字恰能被5整除的概率.
(3)①将(1)中的所得的五位数按从小到大排列,现从中任取5个数,取后放回,所得的5个数中能被5整除的数字的个数X~B(5,$\frac{1}{5}$),由此能求出X的分布列和数学期望.
②所得的五位数按从小到大排列,先求出万位数字是1或3的个数,再求出万位数字是4,千位数字是2的个数,再求出万位数字是4,千位数字是3,百位数字是1的个数,再求出万位数字是4,千位数字是3,百位数字是2且不大于43215的个数,由此能求出“43215”是第几个数.
解答 解:(1)数字1,2,3,4,5能组成:${A}_{5}^{5}$=120没有重复数字的五位数.
(2)数字1,2,3,4,5能组成${A}_{5}^{5}$=120没有重复数字的五位数,
其中能被5整除的有:${A}_{1}^{1}{A}_{4}^{4}$=24个,
∴从(1)中的所得的五位数中任取一个,那么所得数字恰能被5整除的概率:
p=$\frac{24}{120}$=$\frac{1}{5}$.
(3)①将(1)中的所得的五位数按从小到大排列,现从中任取5个数,取后放回,
所得的5个数中能被5整除的数字的个数X~B(5,$\frac{1}{5}$),
P(X=0)=${C}_{5}^{0}(\frac{4}{5})^{5}$=$\frac{1024}{3125}$,
P(X=1)=${C}_{5}^{1}$$(\frac{1}{5})(\frac{4}{5})^{4}$=$\frac{1280}{3125}$,
P(X=2)=${C}_{5}^{2}(\frac{1}{5})^{2}(\frac{4}{5})^{3}$=$\frac{640}{3125}$,
P(X=3)=${C}_{5}^{3}(\frac{1}{5})^{3}(\frac{4}{5})^{2}$=$\frac{160}{3125}$,
P(X=4)=${C}_{5}^{4}(\frac{1}{5})^{4}(\frac{4}{5})$=$\frac{20}{3125}$,
P(X=5)=${C}_{5}^{5}(\frac{1}{5})^{5}$=$\frac{1}{3125}$,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 | 4 | 5 |
| P | $\frac{1024}{3125}$ | $\frac{1280}{3125}$ | $\frac{640}{3125}$ | $\frac{160}{3125}$ | $\frac{20}{3125}$ | $\frac{1}{3125}$ |
点评 本题考查排列数公式的应用,考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
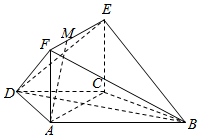 在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°.平面ACEF⊥平面ABCD,四边形ACEF是矩形,AF=a,点M在线段EF上.
在梯形ABCD中,AB∥CD,AD=DC=CB=a,∠ABC=60°.平面ACEF⊥平面ABCD,四边形ACEF是矩形,AF=a,点M在线段EF上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
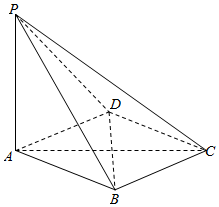 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,AB=2,∠BAD=60°,
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,点O是对角线AC与BD的交点,AB=2,∠BAD=60°,查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥平面ABCD,点E是线段BD的中点,点F是线段PD上的动点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥平面ABCD,点E是线段BD的中点,点F是线段PD上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | 3 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com