
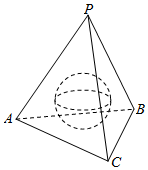
分析 设棱锥底面边长为a,高为h,作过棱锥的高和斜高的截面,根据三角形相似得出a,h的关系,代入棱锥的体积公式,利用导数求出体积的最小值.
解答 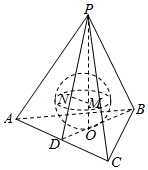 解:设正三棱锥P-ABC的底面边长AB=a,高为PO=h.设内切球球心为M,与平面PAC的切点为N,D为AC的中点,
解:设正三棱锥P-ABC的底面边长AB=a,高为PO=h.设内切球球心为M,与平面PAC的切点为N,D为AC的中点,
则MN⊥PD.DO=$\frac{1}{3}×\frac{\sqrt{3}}{2}a$=$\frac{\sqrt{3}}{6}a$.MN=1,PM=h-1,∴PN=$\sqrt{P{M}^{2}-M{N}^{2}}$=$\sqrt{(h-1)^{2}-1}$=$\sqrt{{h}^{2}-2h}$.
∵Rt△PMN∽Rt△PDO,∴$\frac{MN}{DO}=\frac{PN}{PO}$,即$\frac{1}{\frac{\sqrt{3}}{6}a}=\frac{\sqrt{{h}^{2}-2h}}{h}$,∴a=$\frac{2\sqrt{3}h}{\sqrt{{h}^{2}-2h}}$.
∴$V=\frac{1}{3}•\frac{{\sqrt{3}}}{4}{a^2}•h=\frac{{\sqrt{3}{h^2}}}{h-2}(h>2)$,$V'=\frac{{\sqrt{3}({h^2}-4h)}}{{{{(h-2)}^2}}}$,令V'=0得h=4,
故当h=4时,${V_{min}}=8\sqrt{3}$.
故答案为8$\sqrt{3}$.
点评 本题考查了棱锥与内切球的位置关系,找到底面边长和高的关系是解题的关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com