
���� ��1�������ⷽ�����P�����꣬�õ�ֱ��PA�ķ��̣��ɵ㵽ֱ�ߵľ��빫ʽ���Բ�İ뾶����Բ�ķ��̿���
��2������֪���Բ�ķ��̣���PQ��x��ʱ����kOP•kOQ=-$\frac{3}{4}$���OP��б�ʣ��ɵ�P�����꣬�ɶԳ��Եõ�Q�����꣬��ֱ��PQ��ԲO�ص��ҳ�����PQ��x���ֱʱ����ֱ��PQ�ķ���Ϊy=kx+b����kOP•kOQ=-$\frac{3}{4}$���õ�P��Q������ĺ�����Ĺ�ϵ������ֱ�߷��̺���Բ���̿ɵ�k��b�Ĺ�ϵ�����ɴ�����������ҳ����ֵ���ۺ�����������ֱ��PQ��ԲO�ص��ҳ������ֵ��
��� 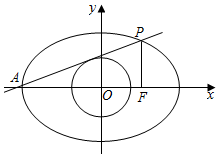 �⣺��1������ԲC�ķ���Ϊ$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1��
�⣺��1������ԲC�ķ���Ϊ$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1��
��A��-2��0����F��1��0����
��PF��x�ᣬ
��P��1��$��\frac{3}{2}$������ֱ��AP��ԲO���У�
���ݶԳ��ԣ���ȡP��1��$\frac{3}{2}$����
��ֱ��AP�ķ���Ϊy=$\frac{1}{2}��x+2��$��
��x-2y+2=0��
��ԲO��ֱ��AP���У���r=$\frac{2}{\sqrt{5}}$��
��ԲO�ķ���Ϊ${x}^{2}+{y}^{2}=\frac{4}{5}$��
��2��������֪��ԲO�ķ���Ϊx2+y2=3��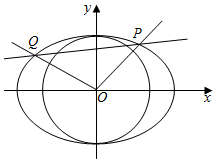
�ٵ�PQ��x��ʱ��${k}_{OP}•{k}_{OQ}=-{{k}_{OP}}^{2}=-\frac{3}{4}$��
��${k}_{OP}=��\frac{\sqrt{3}}{2}$��
������OP��y=$\frac{\sqrt{3}}{2}x$��
����$\left\{\begin{array}{l}{y=\frac{\sqrt{3}}{2}x}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$�����P��$\sqrt{2}$��$\frac{\sqrt{6}}{2}$����
��ʱ��ֱ��PQ��ԲO�صõ��ҳ�Ϊ$\frac{\sqrt{570}}{15}$��
�ڵ�PQ��x���ֱʱ����ֱ��PQ�ķ���Ϊy=kx+b��P��x1��y1����Q��x2��y2����x1x2��0����
������${k}_{OP}•{k}_{OQ}=-\frac{3}{4}$����3x1x+4y1y2=0��
��3x1x2+4��kx1+b����kx2+b��=0��
$��3+4{k}^{2}��{x}_{1}{x}_{2}+4kb��{x}_{1}+{x}_{2}��+4{b}^{2}=0$��*����
����$\left\{\begin{array}{l}{y=kx+b}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$����ȥx���ã�3+4k2��x2+8kbx+4b2-12=0��
��${x}_{1}+{x}_{2}=-\frac{8kb}{3+4{k}^{2}}��{x}_{1}{x}_{2}=\frac{4{b}^{2}-12}{3+4{k}^{2}}$���루*��ʽ����2b2=4k2+3��
����Բ��O��ֱ��PQ�ľ���Ϊ$d=\frac{|b|}{\sqrt{{k}^{2}+1}}$��
��ֱ��PQ��ԲO�صõ��ҳ�Ϊ$l=2\sqrt{3-{d}^{2}}=\sqrt{4+\frac{2}{{k}^{2}+1}}$��
�ʵ�k=0ʱ��l�����ֵΪ$\sqrt{6}$��
���ϣ�ֱ��PQ��ԲO�صõ��ҳ������ֵΪ$\sqrt{6}$��
���� ���⿼����Բ�ļ����ʣ�������ֱ����Բ����Բλ�ù�ϵ��Ӧ�ã������ˡ�������Ľ���˼�뷽������ѧת��˼�뷽�������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 70 | B�� | 168 | C�� | 188 | D�� | 228 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
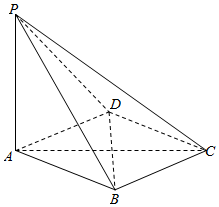 ��ͼ��������P-ABCD�У�PA��ƽ��ABCD������ABCD�����Σ���O�ǶԽ���AC��BD�Ľ��㣬AB=2����BAD=60�㣬
��ͼ��������P-ABCD�У�PA��ƽ��ABCD������ABCD�����Σ���O�ǶԽ���AC��BD�Ľ��㣬AB=2����BAD=60�㣬�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��������P-ABCD�У�����ABCD�������Σ�PD��ƽ��ABCD����E���߶�BD���е㣬��F���߶�PD�ϵĶ��㣮
��ͼ��������P-ABCD�У�����ABCD�������Σ�PD��ƽ��ABCD����E���߶�BD���е㣬��F���߶�PD�ϵĶ��㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
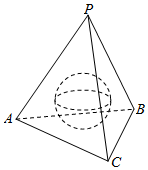
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | 2 | C�� | 3 | D�� | $\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com