
| A. | $\sqrt{2}$x±y=0 | B. | x±$\sqrt{3}$y=0 | C. | x±$\sqrt{2}$y=0 | D. | $\sqrt{3}$x±y=0 |
分析 根据的等边三角形的性质,建立方程关系得到a,b的关系即可求出双曲线的渐近线方程.
解答 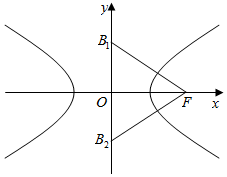 解:∵右焦点F与虚轴的两个端点构成的三角形为等边三角形,
解:∵右焦点F与虚轴的两个端点构成的三角形为等边三角形,
∴tan∠OFB1=tan30°=$\frac{O{B}_{1}}{OF}$,
即$\frac{b}{c}=\frac{\sqrt{3}}{3}$,则b2=$\frac{1}{3}$c2=$\frac{1}{3}$(a2+b2),
即a2=2b2,
则a=$\sqrt{2}$b,
即双曲线的渐近线方程为y=$±\frac{b}{a}x$=±$\frac{\sqrt{2}}{2}$x,
则x±$\sqrt{2}$y=0,
故选:C.
点评 本题主要考查双曲线渐近线的求解,根据正三角形的边长关系建立a,b的关系是解决本题的关键.


科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥平面ABCD,点E是线段BD的中点,点F是线段PD上的动点.
如图,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥平面ABCD,点E是线段BD的中点,点F是线段PD上的动点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,4] | B. | [0,2] | C. | $[{-\frac{3}{2},\frac{5}{2}}]$ | D. | [-4,5] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 36π | B. | 16π | C. | 12π | D. | $\frac{16π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2}$,0)∪(0,2) | B. | (-∞,-$\frac{1}{2}$)∪(2,+∞) | C. | (-$\frac{1}{2}$,0)∪(2,+∞) | D. | (-∞,-$\frac{1}{2}$)∪(0,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com