
【题目】已知数列{an},{bn},满足a1=b1=3,an+1﹣an= ![]() =3,n∈N* , 若数列{cn}满足cn=
=3,n∈N* , 若数列{cn}满足cn= ![]() ,则c2017=( )
,则c2017=( )
A.92016
B.272016
C.92017
D.272017
 培优口算题卡系列答案
培优口算题卡系列答案科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数);以原点
为参数);以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程与曲线
的普通方程与曲线![]() 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若把曲线![]() 各点的横坐标伸长到原来的
各点的横坐标伸长到原来的![]() 倍,纵坐标变为原来的
倍,纵坐标变为原来的![]() ,得到曲线
,得到曲线![]() ,求曲线
,求曲线![]() 的方程;
的方程;
(Ⅲ)设![]() 为曲线
为曲线![]() 上的动点,求点
上的动点,求点![]() 到曲线
到曲线![]() 上点的距离的最小值,并求此时点
上点的距离的最小值,并求此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2018年2月22日,在韩国平昌冬奥会短道速滑男子![]() 米比赛中,中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造了中国男子冰上竞速项目在冬奥会金牌零的突破.根据短道速滑男子
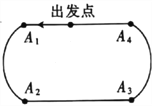
米比赛中,中国选手武大靖以连续打破世界纪录的优异表现,为中国代表队夺得了本届冬奥会的首枚金牌,也创造了中国男子冰上竞速项目在冬奥会金牌零的突破.根据短道速滑男子![]() 米的比赛规则,运动员自出发点出发进入滑行阶段后,每滑行一圈都要依次经过
米的比赛规则,运动员自出发点出发进入滑行阶段后,每滑行一圈都要依次经过![]() 个直道与弯道的交接口
个直道与弯道的交接口![]() .已知某男子速滑运动员顺利通过每个交接口的概率均为
.已知某男子速滑运动员顺利通过每个交接口的概率均为![]() ,摔倒的概率均为
,摔倒的概率均为![]() .假定运动员只有在摔倒或到达终点时才停止滑行,现在用
.假定运动员只有在摔倒或到达终点时才停止滑行,现在用![]() 表示该运动员滑行最后一圈时在这一圈内已经顺利通过的交接口数.
表示该运动员滑行最后一圈时在这一圈内已经顺利通过的交接口数.
(1)求该运动员停止滑行时恰好已顺利通过![]() 个交接口的概率;
个交接口的概率;
(2)求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知a>0,a≠1,设p:函数y=loga(x+3)在(0,+∞)上单调递减,q:函数y=x2+(2a-3)x+1的图像与x轴交于不同的两点.如果p∨q真,p∧q假,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A是抛物线M:y2=2px(p>0)与圆C:x2+(y﹣4)2=a2在第一象限的公共点,且点A到抛物线M焦点F的距离为a,若抛物线M上一动点到其准线与到点C的距离之和的最小值为2a,O为坐标原点,则直线OA被圆C所截得的弦长为( )
A.2
B.2 ![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数f(x)对任意的m,n∈R都有f(m+n)=f(m)+f(n)-1,并且x>0时,恒有f(x)>1.
(1)求证:f(x)在R上是增函数;
(2)若f(3)=4,解不等式f(a2+a-5)<2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆O:x2+y2=4,点F( ![]() ,0),以线段MF为直径的圆内切于圆O,记点M的轨迹为C
,0),以线段MF为直径的圆内切于圆O,记点M的轨迹为C
(1)求曲线C的方程;
(2)若过F的直线l与曲线C交于A,B两点,问:在x轴上是否存在点N,使得 ![]() 为定值?若存在,求出点N坐标;若不存在,说明理由.
为定值?若存在,求出点N坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com