
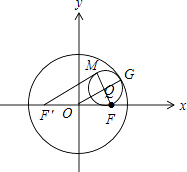
【题目】已知圆O:x2+y2=4,点F( ![]() ,0),以线段MF为直径的圆内切于圆O,记点M的轨迹为C
,0),以线段MF为直径的圆内切于圆O,记点M的轨迹为C
(1)求曲线C的方程;
(2)若过F的直线l与曲线C交于A,B两点,问:在x轴上是否存在点N,使得 ![]() 为定值?若存在,求出点N坐标;若不存在,说明理由.
为定值?若存在,求出点N坐标;若不存在,说明理由.
【答案】
(1)解:设FM的中点为Q,切点为G,连OQ,QG,
则|OQ|+|QG|=|OG|=2,取F关于y轴的对称点F′,连F′M,
故|F′M|+|MF|=2(|OQ|+|QG|)=4.
点M的轨迹是以F′,F为焦点,长轴长为4的椭圆.
其中,a=2,c=,b=1,则曲线C的方程为 ![]() +y2=1
+y2=1
(2)解:当直线l的斜率存在时,设其方程为y=k(x﹣ ![]() ),
),
A(x1,y1),B(x2,y2),
联立 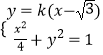 ,得
,得 ![]() .
.
则△>0, ![]() ,
,
若存在定点N(m,0)满足条件,
则有 ![]() =(x1﹣m)(x2﹣m)+y1y2
=(x1﹣m)(x2﹣m)+y1y2
=x1x2+ ![]()
= ![]()
= ![]() =
= ![]() .
.
如果要上式为定值,则必须有 ![]() ,解得m=
,解得m= ![]() ,
,
此时 ![]() =
= ![]() .
.
验证当直线l斜率不存在时,也符合.
故存在点N( ![]() ,0)满足
,0)满足 ![]() 为定值.
为定值.
【解析】(1)设FM的中点为Q,切点为G,连OQ,QG,通过|OQ|+|QG|=|OG|=2,推出|F′M|+|MF|=4.说明点M的轨迹是以F′,F为焦点,长轴长为4的椭圆.然后求解曲线C的方程;(2)当直线l的斜率存在时,设其方程为y=k(x﹣ ![]() ),联立直线方程和椭圆方程,利用根与系数的关系得到A,B的横坐标的和与积,代入
),联立直线方程和椭圆方程,利用根与系数的关系得到A,B的横坐标的和与积,代入 ![]() ,由
,由 ![]() 为定值求得m值,验证斜率不存在时适合得答案.
为定值求得m值,验证斜率不存在时适合得答案.


科目:高中数学 来源: 题型:
【题目】已知数列{an},{bn},满足a1=b1=3,an+1﹣an= ![]() =3,n∈N* , 若数列{cn}满足cn=
=3,n∈N* , 若数列{cn}满足cn= ![]() ,则c2017=( )
,则c2017=( )
A.92016
B.272016
C.92017
D.272017
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国诗词大会》(第二季)亮点颇多,十场比赛每场都有一首特别设计的开场诗词在声光舞美的配合下,百人团齐声朗诵,别有韵味.若《将进酒》《山居秋暝》《望岳《送杜少府之任蜀州》和另确定的两首诗词排在后六场,且《将进酒》排在《望岳》的前面,《山居秋暝》与《送杜少府之任蜀州》不相邻且均不排在最后,则后六场的排法有( )
A. 288种 B. 144种 C. 720种 D. 360种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的定义域是{x|x≠0},对定义域内的任意![]() ,
,![]() 都有f(
都有f(![]() ·
·![]() )=f(
)=f(![]() )+f(
)+f(![]() ),且当x>1时,f(x)>0,f(2)=1.
),且当x>1时,f(x)>0,f(2)=1.
(1)证明:![]() (x)是偶函数;
(x)是偶函数;
(2)证明:![]() (x)在(0,+∞)上是增函数;
(x)在(0,+∞)上是增函数;
(3)解不等式![]() (2
(2![]() -1)<2.
-1)<2.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知O为坐标原点,椭圆C:![]() 的左、右焦点分别为F1,F2,右顶点为A,上顶点为B,若|OB|,|OF2|,|AB|成等比数列,椭圆C上的点到焦点F2的最短距离为
的左、右焦点分别为F1,F2,右顶点为A,上顶点为B,若|OB|,|OF2|,|AB|成等比数列,椭圆C上的点到焦点F2的最短距离为![]() .
.
(1)求椭圆C的标准方程;
(2)设T为直线x=-3上任意一点,过F1的直线交椭圆C于点P,Q,且![]() ,求
,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知两直线l1:ax-by+4=0,l2:(a-1)x+y+b=0.求分别满足下列条件的a,b的值:
(1)直线l1过点(-3,-1),并且直线l1与l2垂直;则a=____,b=_______
(2)直线l1与直线l2平行,并且直线l2在y轴上的截距为3.则a=____,b=_______
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=lnx﹣ ![]() ax2﹣bx
ax2﹣bx
(1)当a=b= ![]() 时,求函数f(x)的单调区间;
时,求函数f(x)的单调区间;
(2)当a=0,b=﹣1时,方程f(x)=mx在区间[1,e2]内有唯一实数解,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点M(3,2)到拋物线C:y=ax2(a>0)准线的距离为4,F为拋物线的焦点,点N(l,l),当点P在直线l:x﹣y=2上运动时, ![]() 的最小值为( )
的最小值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com