
| A. | (-∞,4) | B. | (-∞,4] | C. | (-∞,5) | D. | (-∞,5] |
分析 要使函数f(x)在区间(1,+∞)上是减函数,我们可以转化为f′(x)≤0在区间(1,+∞)上恒成立的问题来求解,然后利用二次函数的单调区间于对称轴的关系来解答也可达到目标.
解答 解:∵函数$f(x)=ax-\frac{1}{2}{x^2}-4lnx$,在区间[1,+∞)上为减函数,
∴f′(x)=-$\frac{4}{x}$-x+a=$\frac{-{x}^{2}+ax-4}{x}$,
由f(x)在区间(1,+∞)上是减函数,可得-x2+ax-4≤0在区间[1,+∞)上恒成立
可得△≤0或$\left\{\begin{array}{l}{\frac{a}{2}≤1}\\{a-5≤0}\end{array}\right.$,即a2-16≤0或a≤2.
解得-4≤a≤4或a≤2,
故a的取值范围为:(-∞,4].
故选:B.
点评 本题以函数为载体,综合考查利用函数的导数来解决有关函数的单调性,考查已知函数的单调性的条件下怎样求解参数的范围问题,考查分类讨论,函数与方程,等数学思想与方法.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
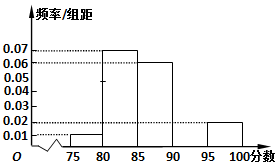 某高校在2016年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.
某高校在2016年的自主招生考试成绩中随机抽取40名学生的笔试成绩,按成绩共分成五组:第1组[75,80),第2组[80,85),第3组[85,90),第4组[90,95),第5组[95,100],得到的频率分布直方图如图所示,同时规定成绩在85分以上的学生为“优秀”,成绩小于85分的学生为“良好”,且只有成绩为“优秀”的学生才能获得面试资格.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $4+2\sqrt{2}$ | B. | $4-2\sqrt{2}$ | C. | $2+\sqrt{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
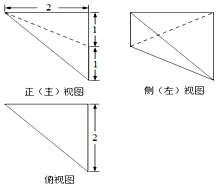
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 1 | D. | $\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com