
| A. | 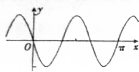 | B. | 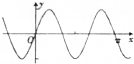 | C. | 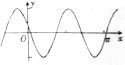 | D. |  |
分析 由函数y=Asin(ωx+φ)的图象变换可得向左平移$\frac{π}{18}$个单位后,得到的函数解析式为:y=-sin3x,利用正弦函数的图象和性质即可得解.
解答 解:将函数y=cos(3x+$\frac{π}{3}$)的图象向左平移$\frac{π}{18}$个单位后,
得到的函数解析式为:y=cos[3(x+$\frac{π}{18}$)+$\frac{π}{3}$]=-sin3x,
此函数过原点,为奇函数,排除C,D;
原点在此函数的单调递减区间上,故排除B.
故选:A.
点评 本题主要考查了函数y=Asin(ωx+φ)的图象变换规律,考查了正弦函数的图象和性质,诱导公式的应用,属于基本知识的考查.


科目:高中数学 来源: 题型:解答题
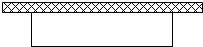 某农场计划使用可以做出30米栅栏的材料,在靠墙(墙足够长)的位置围出一块矩形的菜园(如图).
某农场计划使用可以做出30米栅栏的材料,在靠墙(墙足够长)的位置围出一块矩形的菜园(如图).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 既是奇函数又是偶函数 | B. | 奇函数 | ||
| C. | 既不是奇函数也不是偶函数 | D. | 偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1)∪(2,+∞) | B. | (0,1) | C. | (2,+∞) | D. | (1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com