
【题目】函数y=asinx﹣bcosx的一条对称轴为x= ![]() ,则直线l:ax﹣by+c=0的倾斜角为( )
,则直线l:ax﹣by+c=0的倾斜角为( )
A.45°
B.60°
C.120°
D.135°
【答案】D
【解析】解:f(x)=asinx﹣bcosx,
∵对称轴方程是x= ![]() ,
,
∴f( ![]() +x)=f(
+x)=f( ![]() ﹣x) 对任意x∈R恒成立,
﹣x) 对任意x∈R恒成立,
asin( ![]() +x)﹣bcos(
+x)﹣bcos( ![]() +x)=asin(
+x)=asin( ![]() ﹣x)﹣bcos(
﹣x)﹣bcos( ![]() ﹣x),
﹣x),
asin( ![]() +x)﹣asin(
+x)﹣asin( ![]() ﹣x)=bcos(
﹣x)=bcos( ![]() +x)﹣bcos(
+x)﹣bcos( ![]() ﹣x),
﹣x),
用加法公式化简:
2acos ![]() sinx=﹣2bsin
sinx=﹣2bsin ![]() sinx 对任意x∈R恒成立,
sinx 对任意x∈R恒成立,
∴(a+b)sinx=0 对任意x∈R恒成立,
∴a+b=0,
∴直线ax﹣by+c=0的斜率K= ![]() =﹣1,
=﹣1,
∴直线ax﹣by+c=0的倾斜角为 ![]() =135°.
=135°.
故选D.
【考点精析】解答此题的关键在于理解直线的倾斜角的相关知识,掌握当直线l与x轴相交时, 取x轴作为基准, x轴正向与直线l向上方向之间所成的角α叫做直线l的倾斜角.特别地,当直线l与x轴平行或重合时, 规定α=0°.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】已知函数g(x)满足g(x)=g′(1)ex﹣1﹣g(0)x+ ![]() ,且存在实数x0使得不等式2m﹣1≥g(x0)成立,则m的取值范围为( )
,且存在实数x0使得不等式2m﹣1≥g(x0)成立,则m的取值范围为( )
A.(﹣∞,2]
B.(﹣∞,3]
C.[1,+∞)
D.[0,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线系M:xcosθ+ysinθ=1,对于下列四个命题:
①不在直线系M中的点都落在面积为π的区域内
②直线系M中所有直线为一组平行线
③直线系M中所有直线均经过一个定点
④对于任意整数n(n≥3),存在正n边形,其所有边均在直线系M中的直线上
其中真命题的代号是(写出所有真命题的代号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校高二(1)班的一次数学测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏,但可见部分如图,且将全班25人的成绩记为AI(I=1,2,…,25)由右边的程序运行后,输出n=10.据此解答如下问题: 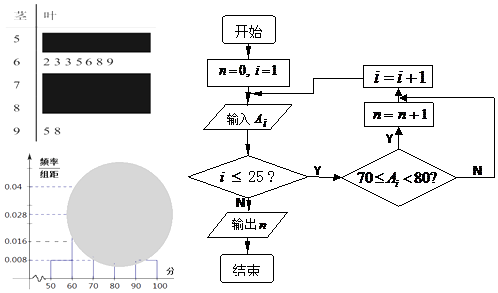
(Ⅰ)求茎叶图中破损处分数在[50,60),[70,80),[80,90)各区间段的频数;
(Ⅱ)利用频率分布直方图估计该班的数学测试成绩的众数,中位数分别是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F为抛物线y2=x的焦点,点A,B在该抛物线上且位于x轴的两侧, ![]() =2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
=2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
A.2
B.3
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面有五个命题:
①函数y=sin4x﹣cos4x的最小正周期是π;
② ![]() =tanα;
=tanα;
③函数y=sinx+cosx的图象均关于点( ![]() ,0)成中心对称;
,0)成中心对称;
④把函数y=3sin(2x+ ![]() )的图象向右平移
)的图象向右平移 ![]() 个单位得到y=3sin2x的图象.
个单位得到y=3sin2x的图象.
其中正确命题的编号是 . (写出所有正确命题的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,已知角A、B、C所对的边分别为a、b、c,且a2+b2﹣c2= ![]() ab.
ab. 
(1)求角C的大小;
(2)如果0<A≤ ![]() ,m=2cos2
,m=2cos2 ![]() ﹣sinB﹣1,求实数m的取值范围.
﹣sinB﹣1,求实数m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com