
分析 (1)由数列的前n项和求出首项,并求出n≥2时的通项,验证首项后得答案;
(2)由${S}_{{k}^{2}}=({S}_{k})^{2}$,得$\frac{1}{2}{k}^{4}+{k}^{2}=(\frac{1}{2}{k}^{2}+k)^{2}$,解方程即可求得k值;
(3)设数列{an}的公差为d,则在${S_{n^2}}={({S_n})^2}$中分别取k=1,2,求得首项和公差,验证是否满足${S}_{{n}^{2}}=({S}_{n})^{2}$成立得答案.
解答 解:(1)当n=1时,a1=S1=$\frac{3}{2}$;
当n≥2时an=Sn-Sn-1 =$\frac{1}{2}$n2+n-[$\frac{1}{2}(n-1)^{2}+(n-1)$]=n+$\frac{1}{2}$.
n=1时,${a_1}=\frac{3}{2}$,满足上式.
∴${a_n}=n+\frac{1}{2}$;
(2)∵Sn=$\frac{1}{2}$n2+n,
∴由${S}_{{k}^{2}}=({S}_{k})^{2}$,得$\frac{1}{2}{k}^{4}+{k}^{2}=(\frac{1}{2}{k}^{2}+k)^{2}$,
即$\frac{1}{4}{k}^{4}={k}^{3}$,又k≠0,∴k=4;
(3)设数列{an}的公差为d,则在${S_{n^2}}={({S_n})^2}$中分别取k=1,2,得
$\left\{\begin{array}{l}{{S}_{1}=({S}_{1})^{2}}\\{{S}_{4}=({S}_{2})^{2}}\end{array}\right.$,即$\left\{\begin{array}{l}{{a}_{1}={{a}_{1}}^{2}①}\\{4{a}_{1}+\frac{4×3}{2}d=(2{a}_{1}+\frac{2×1}{2}d)^{2}②}\end{array}\right.$
由①得:a1=0或a1=1.
当a1=0时,代入②得:d=0或d=6,
若a1=d=0,则an=Sn=0,从而${S}_{{k}^{2}}=({S}_{k})^{2}$成立;
若a1=0,d=6,则an=6(n-1),由${S}_{3}=18,({S}_{3})^{2}=324$,S9=216,知${S}_{9}≠({S}_{3})^{2}$,
故所得数列不符合题意;
当a1=1时,代入②得:4+6d=(2+d)2,解得d=0或d=2.
若a1=1,d=0,则an=1,Sn=n,从而${S}_{{k}^{2}}=({S}_{k})^{2}$成立;
若a1=1,d=2,则${a}_{n}=2n-1,{S}_{n}=1+3+…+(2n-1)={n}^{2}$,
从而${S}_{{n}^{2}}=({S}_{n})^{2}$成立.
综上,共有3个满足条件的无穷等差数列:
①{an}:an=0,即0,0,0,…;
②{an}:an=1,即1,1,1,…;
③{an}:an=2n-1,即1,3,5,….
点评 本题考查数列的和,考查了等差关系的确定,考查学生的逻辑思维能力和推理论证能力,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
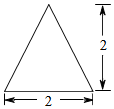 一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示,则该四棱锥的侧面积是( )
一个四棱锥的侧棱长都相等,底面是正方形,其正(主)视图如图所示,则该四棱锥的侧面积是( )| A. | $4\sqrt{3}$ | B. | $4\sqrt{5}$ | C. | $4({\sqrt{5}+1})$ | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 椭圆的一部分 | B. | 双曲线的一部分 | C. | 抛物线的一部分 | D. | 直线的一部分 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
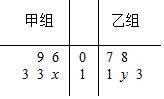 为了研究学生在考试时做解答题的情况,老师从甲、乙两个班级里各随机抽取了五份答卷并对解答题第16题(满分13分)的得分进行统计,得到对应的甲、乙两组数据,其茎叶图如图所示,其中x,y∈{0,1,2,3},已知甲组数据的中位数比乙组数据的平均数多$\frac{9}{5}$,则x+y的值为( )
为了研究学生在考试时做解答题的情况,老师从甲、乙两个班级里各随机抽取了五份答卷并对解答题第16题(满分13分)的得分进行统计,得到对应的甲、乙两组数据,其茎叶图如图所示,其中x,y∈{0,1,2,3},已知甲组数据的中位数比乙组数据的平均数多$\frac{9}{5}$,则x+y的值为( )| A. | 5 | B. | 4 | C. | 3 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com