
分析 由已知得到$\overrightarrow{a}$-2$\overrightarrow{{e}_{1}}$=$\overrightarrow{{e}_{2}}$,然后利用向量在向量方向上的投影公式求得答案.
解答 解:∵$\overrightarrow{a}$=2$\overrightarrow{{e}_{1}}$+$\overrightarrow{{e}_{2}}$,∴$\overrightarrow{a}$-2$\overrightarrow{{e}_{1}}$=$\overrightarrow{{e}_{2}}$,
又向量$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$为单位向量且夹角为60°,
∴$\overrightarrow{a}$在$\overrightarrow{a}$-2$\overrightarrow{{e}_{1}}$方向上的投影为:
$\frac{\overrightarrow{a}•(\overrightarrow{a}-2\overrightarrow{{e}_{1}})}{|\overrightarrow{a}-2\overrightarrow{{e}_{1}}|}$=$\frac{(2\overrightarrow{{e}_{1}}+\overrightarrow{{e}_{2}})•\overrightarrow{{e}_{2}}}{|\overrightarrow{{e}_{2}}|}$=$2\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}+|\overrightarrow{{e}_{2}}{|}^{2}$=2×1×1×cos60°+1=2.
故答案为:2.
点评 本题考查平面向量的数量积运算,考查了向量在向量方向上的投影的概念,是中档题.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:解答题
| x 人数 y | A | B | C |
| A | l4 | 40 | 10 |
| B | a | 36 | b |
| C | 28 | 8 | 34 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
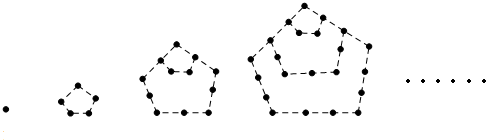
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 7 | C. | 8 | D. | 9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com