
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
分析 根据题意,设木棒长度为1,折成两段后,其中一段长度为x,可求得另一段长度1-x,求出所有的基本事件构成的区域长度为1,根据题意列出不等关系求出事件“其中一段长度大于另一段长度3倍”构成的区域长度,利用几何概型概率公式求出事件的概率.
解答 解:设总长度是1,一段是x,则另一段是1-x,
由题意得:x>3(1-x)或1-x>3x,
解得:x>$\frac{3}{4}$或x<$\frac{1}{4}$,
故满足条件的概率是p=$\frac{(1-\frac{3}{4})+\frac{1}{4}}{1}$=$\frac{1}{2}$,
故选:C.
点评 本题考查几何概型的计算,关键根据题意列出不等关系求出事件A构成的区域长度.


科目:高中数学 来源: 题型:选择题
| A. | (1,-1) | B. | (1,1) | C. | (-1,1) | D. | (-1,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (0,1] | C. | (-1,1) | D. | (-1,0] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
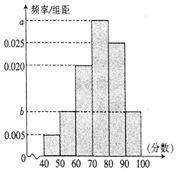 某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列.
某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:[40,50),[50,60),…,[90,100]后得到如图所示的频率分布直方图,其中前三段的频率成等比数列.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨q | B. | (¬p)∨q | C. | (¬p)∧q | D. | (¬p)∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com