Question

15．已知抛物线y=$\frac{{x}^{2}}{4}$与直线y=$\frac{3}{4}$x+1交于点P，Q，则如图所示阴影部分的面积为（　　）

• A． $\frac{65}{12}$
• B． $\frac{85}{16}$
• C． $\frac{143}{24}$
• D． $\frac{95}{6}$

Answer 1

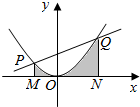
分析 根据方程组得解求出积分上下限，再根据定积分的应用得到则所示阴影部分的面积S=${∫}_{-1}^{4}$$\frac{{x}^{2}}{4}$dx，求定积分即可．

解答 解：联立方程组得$\left\{\begin{array}{l}{y=\frac{{x}^{2}}{4}}\\{y=\frac{3}{4}x+1}\end{array}\right.$，
解得$\left\{\begin{array}{l}{x=-1}\\{y=\frac{1}{4}}\end{array}\right.$或$\left\{\begin{array}{l}{x=4}\\{y=4}\end{array}\right.$，
∴抛物线y=$\frac{{x}^{2}}{4}$与直线y=$\frac{3}{4}$x+1交于点P，Q，则所示阴影部分的面积S=${∫}_{-1}^{4}$$\frac{{x}^{2}}{4}$dx=$\frac{{x}^{3}}{12}$|${\;}_{-1}^{4}$=$\frac{64}{12}$+$\frac{1}{12}$=$\frac{65}{12}$，
故选：A．

点评 本题考查了定积分在求面积中的应用，属于基础题．