
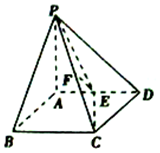
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,且PA=AD=2,BD=2$\sqrt{2}$,E、F分别为AD、PC中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,且PA=AD=2,BD=2$\sqrt{2}$,E、F分别为AD、PC中点.分析 (1)取PB的中点G,连接FG、AG,证得底面ABCD为正方形.再由中位线定理可得FG∥AE且FG=AE,四边形AEFG是平行四边形,则AG∥FE,运用线面平行的判定定理可得EF∥平面PAB,点F与点E到平面PAB的距离相等,运用线面垂直的判定和性质,证得AD⊥平面PAB,即可得到所求距离;
(2)运用线面垂直的判定和性质,证得BC⊥平面PAB,EF⊥平面PBC,再由面面垂直的判定定理,即可得证.
解答 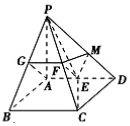 (1)解:如图,取PB的中点G,连接FG、AG,
(1)解:如图,取PB的中点G,连接FG、AG,
因为底面ABCD为菱形,且PA=AD=2,$BD=2\sqrt{2}$,
所以底面ABCD为正方形.
∵E、F分别为AD、PC中点,
∴FG∥BC,AE∥BC,$FG=\frac{1}{2}BC$,$AE=\frac{1}{2}AD$,
∴FG∥AE且FG=AE,
∴四边形AEFG是平行四边形,∴AG∥FE,
∵AG?平面PAB,EF?平面PAB,∴EF∥平面PAB,
∴点F与点E到平面PAB的距离相等,
由PA⊥平面ABCD,可得PA⊥AD,
又AD⊥AB,PA∩AB=A,
AD⊥平面PAB,
则点F到平面PAB的距离为EA=1.
(2)证明:由(1)知AG⊥PB,AG∥EF,
∵PA⊥平面ABCD,∴BC⊥PA,
∵BC⊥AB,AB∩BC=B,∴BC⊥平面PAB,
由AG?平面PAB,
∴BC⊥AG,又∵PB∩BC=B,
∴AG⊥平面PBC,∴EF⊥平面PBC,
∵EF?平面PCE,
∴平面PCE⊥平面PBC.
点评 本题考查空间点到平面的距离,注意运用转化思想,考查线面平行和垂直的判定和性质,以及面面垂直的判定,熟练掌握定理的条件和结论是解题的关键,属于中档题.


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:高中数学 来源: 题型:解答题
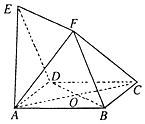 如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC,AC、BD交于点O.
如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC,AC、BD交于点O.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
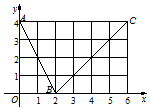 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(1)+f(3)=( )
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(1)+f(3)=( )| A. | 3 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
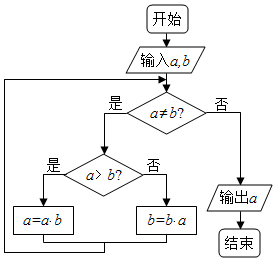 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b分别为2,8,则输出的a等于( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入a,b分别为2,8,则输出的a等于( )| A. | 4 | B. | 0 | C. | 14 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
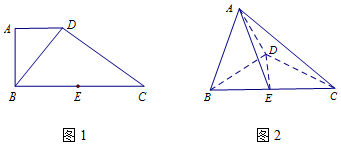
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1种 | B. | 2种 | C. | 3种 | D. | 4种 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2米/秒 | B. | 3米/秒 | C. | 4米/秒 | D. | 5米/秒 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com