
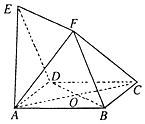
 如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC,AC、BD交于点O.
如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC,AC、BD交于点O.分析 (Ⅰ)因为四边形ABCD与BDEF均为菱形,所以AD∥BC,DE∥BF,可得平面FBC∥平面EAD,由此能够证明FC∥平面EAD;
(Ⅱ)设AC与BD相交于点O,连接FO,推导出AC⊥BD,AC⊥FO,由此能证明AC⊥平面BDEF;
(Ⅲ)连接FO、FD,先证明FO⊥平面ABCD.,再过O作OH垂直AB于H,连结FH,则∠FHO就是二面角F-AB-C(锐角)的平面角.
解答 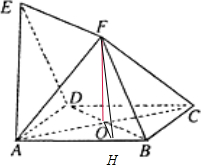 解:(Ⅰ)证明:因为四边形ABCD与BDEF均为菱形,
解:(Ⅰ)证明:因为四边形ABCD与BDEF均为菱形,
所以AD∥BC,DE∥BF.
因为AD?平面FBC,DE?平面FBC,所以AD∥平面FBC,DE∥平面FBC
又AD∩DE=D,AD?平面EAD,DE?平面EAD,所以平面FBC∥平面EAD
又FC?平面FBC,所以FC∥平面EAD
(Ⅱ)证明:连接FO,因为四边形ABCD为菱形,所以AC⊥BD,
又O为AC中点,且FA=FC,所以AC⊥FO,
因为FO∩BD=O,所以AC⊥平面BDEF.
(Ⅲ)连接FO、FD,则因为四边形BDEF为菱形,且∠DBF=60°,
所以△DBF为等边三角形,
因为O为BD中点.所以FO⊥BD,又因为O为AC中点,且FA=FC,所以AC⊥FO
又AC∩BD=O,所以FO⊥平面ABCD.
过O作OH垂直AB于H,连结FH,则∠FHO就是二面角F-AB-C(锐角)的平面角.
设AB=2,因为四边形ABCD为菱形,∠DAB=60°,则BD=2,OB=1,FO=$\sqrt{3}$,
OH=$\frac{1}{2}ADsin6{0}^{0}=\frac{\sqrt{3}}{2}$,tan∠FHO=$\frac{OF}{OH}=2$,∴$cos∠FHO=\frac{\sqrt{5}}{5}$,
二面角F-AB-C(锐角)的余弦值为$\frac{\sqrt{5}}{5}$.
点评 本题考查直线与平面垂直、直线与平面平行的证明,考查二面角的余弦值的求法,考查学生分析解决问题的能力,属于中档题..


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}π$ | B. | $\frac{8}{3}π$ | C. | $\frac{10}{3}π$ | D. | $\frac{16}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
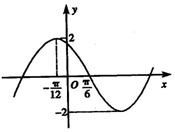 已知函数f(x)=2sin(ωx+φ)(x∈R,ω>0,-π<φ<π)的部分图象如图所示,若将函数f(x)的图象向右平移$\frac{π}{6}$个单位得到函数g(x)的图象,则函数g(x)的解析式是g(x)=2sin(2x+$\frac{π}{3}$).
已知函数f(x)=2sin(ωx+φ)(x∈R,ω>0,-π<φ<π)的部分图象如图所示,若将函数f(x)的图象向右平移$\frac{π}{6}$个单位得到函数g(x)的图象,则函数g(x)的解析式是g(x)=2sin(2x+$\frac{π}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
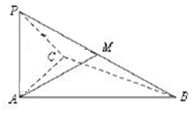 如图,已知三棱锥P-ABC,PA⊥平面ABC,∠ACB=90°,∠BAC=60°,PA=AC,M为PB的中点.
如图,已知三棱锥P-ABC,PA⊥平面ABC,∠ACB=90°,∠BAC=60°,PA=AC,M为PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
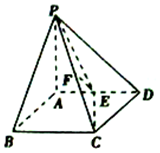 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,且PA=AD=2,BD=2$\sqrt{2}$,E、F分别为AD、PC中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,且PA=AD=2,BD=2$\sqrt{2}$,E、F分别为AD、PC中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com