
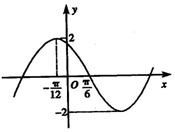
 已知函数f(x)=2sin(ωx+φ)(x∈R,ω>0,-π<φ<π)的部分图象如图所示,若将函数f(x)的图象向右平移$\frac{π}{6}$个单位得到函数g(x)的图象,则函数g(x)的解析式是g(x)=2sin(2x+$\frac{π}{3}$).
已知函数f(x)=2sin(ωx+φ)(x∈R,ω>0,-π<φ<π)的部分图象如图所示,若将函数f(x)的图象向右平移$\frac{π}{6}$个单位得到函数g(x)的图象,则函数g(x)的解析式是g(x)=2sin(2x+$\frac{π}{3}$). 分析 通过函数的图象求出A,求出函数的周期,利用周期公式求出ω,函数过(-$\frac{π}{12}$,2),结合φ的范围,求出φ,推出函数的解析式,通过函数图象的平移推出结果.
解答 解:∵由图象知A=2,$\frac{1}{4}$T=$\frac{π}{6}$-(-$\frac{π}{12}$)=$\frac{π}{4}$,
∴T=π⇒ω=2,
∵2sin[2×(-$\frac{π}{12}$)+φ]=2,
∴可得:2×(-$\frac{π}{12}$)+φ=2kπ$+\frac{π}{2}$,k∈Z,
∵-π<φ<π,
∴得:φ=$\frac{2π}{3}$,可得:f(x)=2sin(2x+$\frac{2π}{3}$),
∴则图象向右平移$\frac{π}{6}$个单位后得到的图象解析式为g(x)=2sin[2(x-$\frac{π}{6}$)+$\frac{2π}{3}$]=2sin(2x+$\frac{π}{3}$),
故答案为:g(x)=2sin(2x+$\frac{π}{3}$).
点评 本题考查学生的识图能力,函数的解析式的求法,图象的变换,考查计算能力,属于基本知识的考查.


 53随堂测系列答案
53随堂测系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
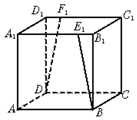 如图,ABCD-A1B1C1D1是正方体,${B_1}{E_1}={D_1}{F_1}=\frac{{{A_1}{B_1}}}{4}$,则BE1与DF1所成角的余弦值是$\frac{15}{17}$.
如图,ABCD-A1B1C1D1是正方体,${B_1}{E_1}={D_1}{F_1}=\frac{{{A_1}{B_1}}}{4}$,则BE1与DF1所成角的余弦值是$\frac{15}{17}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
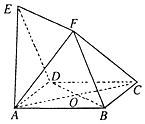 如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC,AC、BD交于点O.
如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC,AC、BD交于点O.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
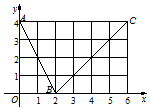 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(1)+f(3)=( )
如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则f(1)+f(3)=( )| A. | 3 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com