
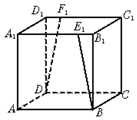
 如图,ABCD-A1B1C1D1是正方体,${B_1}{E_1}={D_1}{F_1}=\frac{{{A_1}{B_1}}}{4}$,则BE1与DF1所成角的余弦值是$\frac{15}{17}$.
如图,ABCD-A1B1C1D1是正方体,${B_1}{E_1}={D_1}{F_1}=\frac{{{A_1}{B_1}}}{4}$,则BE1与DF1所成角的余弦值是$\frac{15}{17}$. 分析 建立空间直角坐标系,设正方体的边长为1,表示出向量$\overrightarrow{{BE}_{1}}$、$\overrightarrow{{DF}_{1}}$,求出$\overrightarrow{{BE}_{1}}$、$\overrightarrow{{DF}_{1}}$所成角的余弦值即可.
解答 解:建立空间直角坐标系如图所示,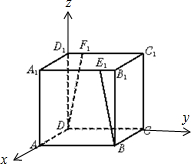
设正方体的边长为1,由${B_1}{E_1}={D_1}{F_1}=\frac{{{A_1}{B_1}}}{4}$,
则B(1,1,0),D(0,0,0),
E1(1,$\frac{3}{4}$,1),F1(0,$\frac{1}{4}$,1),
则$\overrightarrow{{BE}_{1}}$=(0,-$\frac{1}{4}$,1),
$\overrightarrow{{DF}_{1}}$=(0,$\frac{1}{4}$,1),
$\overrightarrow{{BE}_{1}}$•$\overrightarrow{{DF}_{1}}$=-$\frac{1}{16}$+1=$\frac{15}{16}$,
|$\overrightarrow{{BE}_{1}}$|=|$\overrightarrow{{DF}_{1}}$|=$\sqrt{\frac{1}{16}+1}$=$\frac{\sqrt{17}}{4}$;
∴$\overrightarrow{{BE}_{1}}$、$\overrightarrow{{DF}_{1}}$所成角的余弦值是:
cosθ=$\frac{\overrightarrow{{BE}_{1}}•\overrightarrow{{DF}_{1}}}{|\overrightarrow{{BE}_{1}}|×|\overrightarrow{{DF}_{1}}|}$=$\frac{\frac{15}{16}}{\frac{\sqrt{17}}{4}×\frac{\sqrt{17}}{4}}$=$\frac{15}{17}$.
故答案为:$\frac{15}{17}$.
点评 本题考查了空间两条直线所成角的运算问题,可以利用空间向量进行求解,是基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图1,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于点A,将△PAD沿AD折起,构成如图2所示的四棱锥P-ABCD,点M的棱PB上,且PM=$\frac{1}{2}$MB.
如图1,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于点A,将△PAD沿AD折起,构成如图2所示的四棱锥P-ABCD,点M的棱PB上,且PM=$\frac{1}{2}$MB.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
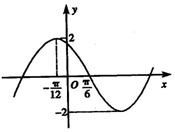 已知函数f(x)=2sin(ωx+φ)(x∈R,ω>0,-π<φ<π)的部分图象如图所示,若将函数f(x)的图象向右平移$\frac{π}{6}$个单位得到函数g(x)的图象,则函数g(x)的解析式是g(x)=2sin(2x+$\frac{π}{3}$).
已知函数f(x)=2sin(ωx+φ)(x∈R,ω>0,-π<φ<π)的部分图象如图所示,若将函数f(x)的图象向右平移$\frac{π}{6}$个单位得到函数g(x)的图象,则函数g(x)的解析式是g(x)=2sin(2x+$\frac{π}{3}$).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com