练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．若复数$\frac{a+i}{1+2i}$（a∈R）为纯虚数，其中i为虚数单位，则a=（　　）
    A．-3B．-2C．2D．3

    分析 由复数代数形式的乘除运算化简复数$\frac{a+i}{1+2i}$，又根据复数$\frac{a+i}{1+2i}$（a∈R）为纯虚数，列出方程组，求解即可得答案．

    解答 解：$\frac{a+i}{1+2i}$=$\frac{（a+i）（1-2i）}{（1+2i）（1-2i）}=\frac{（2+a）+（1-2a）i}{5}$=$\frac{2+a}{5}+\frac{1-2a}{5}i$，
    ∵复数$\frac{a+i}{1+2i}$（a∈R）为纯虚数，
    ∴$\left\{\begin{array}{l}{\frac{2+a}{5}=0}\\{\frac{1-2a}{5}≠0}\end{array}\right.$，
    解得：a=-2．
    故选：B．

    点评 本题考查了复数代数形式的乘除运算，考查了复数的基本概念，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    5．已知圆C：x2+y2+4x+3=0，若直线y=kx-1上至少存在一点，使得以该点为圆心，1为半径的圆与圆C有公共点，则实数k的取值范围为-$\frac{4}{3}$≤k≤0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

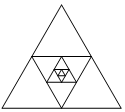    6．如图，画一个边长为2的正三角形，再将这个正三角形各边的中点相连得到第二个正三角形，依此类推，一共画了5个正三角形．那么这五个正三角形的面积之和等于（　　）
    A．2$\sqrt{3}$B．$\frac{21}{16}$$\sqrt{3}$C．$\frac{85}{64}$$\sqrt{3}$D．$\frac{341}{256}$$\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．设x，y满足约束条件$\left\{\begin{array}{l}x≥0，y≥0\\ x-y≥-1\\ x+y≤3\end{array}\right.$，则z=2x-y的最大值为（　　）
    A．0B．2C．-2D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．在直角坐标系中，以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为ρ-2cosθ-6sinθ+$\frac{1}{ρ}$=0，直线l的参数方程为$\left\{\begin{array}{l}{x=3+\frac{1}{2}t}\\{y=3+\frac{\sqrt{3}}{2}t}\end{array}\right.$（t为参数）．
    （1）求曲线C的普通方程；
    （2）若直线l与曲线C交于A，B两点，点P的坐标为（3，3），求|PA|+|PB|的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    20．已知α是锐角，且cos（α+$\frac{π}{6}$）=$\frac{1}{3}$，则cos（α-$\frac{π}{3}$）=$\frac{2\sqrt{2}}{3}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

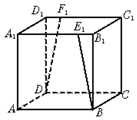    7．如图，ABCD-A1B1C1D1是正方体，${B_1}{E_1}={D_1}{F_1}=\frac{{{A_1}{B_1}}}{4}$，则BE1与DF1所成角的余弦值是$\frac{15}{17}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．已知定义域为R的函数f（x）满足下列性质：f（x+1）=f（-x-1），f（2-x）=-f（x） 则f（3）=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．如图所示的程序框图，若输出的结果为21，则判断框中应填入（　　）
    A．k≤2？B．k≤3？C．k≤4？D．k≤5？

    查看答案和解析>>

    同步练习册答案