
分析 由已知利用诱导公式可求sin(α-$\frac{π}{3}$)=$\frac{1}{3}$,结合角的范围,利用同角三角函数基本关系式计算可解.
解答 解:∵cos(α+$\frac{π}{6}$)=sin[$\frac{π}{2}$-(α+$\frac{π}{6}$)]=sin(α-$\frac{π}{3}$)=$\frac{1}{3}$,
∵α是锐角,α-$\frac{π}{3}$∈(-$\frac{π}{3}$,$\frac{π}{6}$),
∴cos(α-$\frac{π}{3}$)=$\sqrt{1-si{n}^{2}(α-\frac{π}{3})}$=$\sqrt{1-(\frac{1}{3})^{2}}$=$\frac{2\sqrt{2}}{3}$.
故答案为:$\frac{2\sqrt{2}}{3}$.
点评 本题主要考查了诱导公式,同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
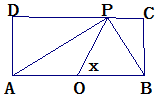 如图,长方形的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD,与DA运动,记∠BOP=x,将动点P到A,B两点距离之和表示为函数f(x),则f(x)的图象大致为( )
如图,长方形的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD,与DA运动,记∠BOP=x,将动点P到A,B两点距离之和表示为函数f(x),则f(x)的图象大致为( )| A. | 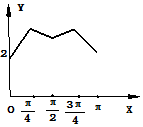 | B. | 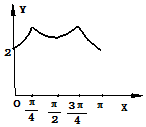 | ||
| C. | 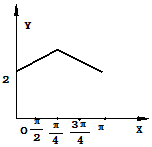 | D. | 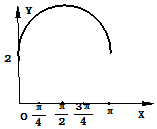 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 10 | C. | 8 | D. | 2+log35 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图1,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于点A,将△PAD沿AD折起,构成如图2所示的四棱锥P-ABCD,点M的棱PB上,且PM=$\frac{1}{2}$MB.
如图1,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于点A,将△PAD沿AD折起,构成如图2所示的四棱锥P-ABCD,点M的棱PB上,且PM=$\frac{1}{2}$MB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{\sqrt{2}}{2}$,1) | B. | ($\frac{1}{2}$,1) | C. | (0,$\frac{\sqrt{2}}{2}$) | D. | (0,$\frac{1}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com