
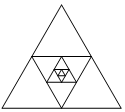
 如图,画一个边长为2的正三角形,再将这个正三角形各边的中点相连得到第二个正三角形,依此类推,一共画了5个正三角形.那么这五个正三角形的面积之和等于( )
如图,画一个边长为2的正三角形,再将这个正三角形各边的中点相连得到第二个正三角形,依此类推,一共画了5个正三角形.那么这五个正三角形的面积之和等于( )| A. | 2$\sqrt{3}$ | B. | $\frac{21}{16}$$\sqrt{3}$ | C. | $\frac{85}{64}$$\sqrt{3}$ | D. | $\frac{341}{256}$$\sqrt{3}$ |
分析 此五个正三角形的边长an形成等比数列:2,1,$\frac{1}{2}$,$\frac{1}{4}$,$\frac{1}{8}$.再利用等比数列的求和公式即可得出这五个正三角形的面积之和.
解答 解:此五个正三角形的边长an形成等比数列:2,1,$\frac{1}{2}$,$\frac{1}{4}$,$\frac{1}{8}$.
∴这五个正三角形的面积之和=$\frac{\sqrt{3}}{4}$×$({2}^{2}+{1}^{2}+\frac{1}{{2}^{2}}+\frac{1}{{2}^{4}}+\frac{1}{{2}^{6}})$
=$\frac{\sqrt{3}}{4}×\frac{4×(1-\frac{1}{{4}^{5}})}{1-\frac{1}{4}}$
=$\frac{341}{256}\sqrt{3}$.
故选:D.
点评 本题考查了等边三角形的性质与面积计算公式、等比数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
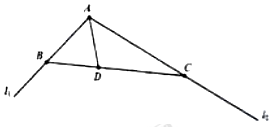 某市渭河的某水域有夹角为120°的两条直线河岸l1,l2(如图所示):在该水域中,位于该角平分线且距A地相距1公里的D处有座千年古亭,为保护古亭,沿D所在直线BC建一河堤(B,C分别在l1,l2上,河堤下方有进、出水的桥洞);现要在△ABC水域建一个水上游乐城,如何设计AB、AC河岸的长度,AB、AC都不超过5公里(不妨令AB=x公里,AC=y公里).
某市渭河的某水域有夹角为120°的两条直线河岸l1,l2(如图所示):在该水域中,位于该角平分线且距A地相距1公里的D处有座千年古亭,为保护古亭,沿D所在直线BC建一河堤(B,C分别在l1,l2上,河堤下方有进、出水的桥洞);现要在△ABC水域建一个水上游乐城,如何设计AB、AC河岸的长度,AB、AC都不超过5公里(不妨令AB=x公里,AC=y公里).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{3}π$ | B. | $\frac{8}{3}π$ | C. | $\frac{10}{3}π$ | D. | $\frac{16}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
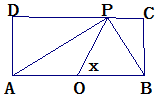 如图,长方形的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD,与DA运动,记∠BOP=x,将动点P到A,B两点距离之和表示为函数f(x),则f(x)的图象大致为( )
如图,长方形的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD,与DA运动,记∠BOP=x,将动点P到A,B两点距离之和表示为函数f(x),则f(x)的图象大致为( )| A. | 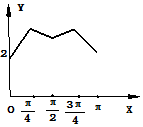 | B. | 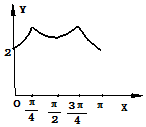 | ||
| C. | 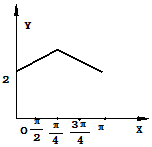 | D. | 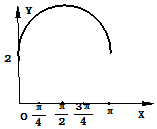 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com