
分析 (1)由题意直接写出曲线C的参数方程,消去参数t可得直线l的普通方程;
(2)设点P的坐标为(2cosθ,3sinθ),由点到直线的距离公式表示出点P到直线l的距离d,由辅助角公式化简后,由正弦函数的最值求出点P到直线l的距离的最大值及最小值.
解答 解:(1)∵曲线C:$\frac{x^2}{4}+\frac{y^2}{9}=1$,
∴曲线C的参数方程为:$\left\{{\begin{array}{l}{x=2cosθ}\\{y=3sinθ}\end{array}}\right.$(θ为参数),
∵直线l:$\left\{{\begin{array}{l}{x=2+t}\\{y=2-2t}\end{array}}\right.(t为参数)$.
∴消去t得,直线l的普通方程为:2x+y-6=0;(5分)
(2)设点P的坐标为(2cosθ,3sinθ),则点P到直线l的距离设为d,
则$d=\frac{{|{4cosθ+3sinθ-6}|}}{{\sqrt{5}}}=\frac{{\sqrt{5}|{6-5sin(θ+ϕ)}|}}{5}$(其中$tanϕ=\frac{4}{3}$)
∵-1≤sin(θ+φ)≤1,
∴${d_{max}}=\frac{{11\sqrt{5}}}{5}$,${d_{min}}=\frac{{\sqrt{5}}}{5}$,
即点P到直线l的距离的最大值及最小值分别为:$\frac{11\sqrt{5}}{5}$、$\frac{\sqrt{5}}{5}$.(10分)
点评 本题考查参数方程与普通方程的转化,点到直线的距离公式,辅助角公式,以及正弦函数的最值的应用,考查化简、变形能力.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要 | B. | 必要不充分 | C. | 充要 | D. | 非充分非必要 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≥1 | B. | m≥2 | C. | m≥3 | D. | m≥4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
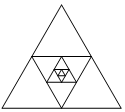 如图,画一个边长为2的正三角形,再将这个正三角形各边的中点相连得到第二个正三角形,依此类推,一共画了5个正三角形.那么这五个正三角形的面积之和等于( )
如图,画一个边长为2的正三角形,再将这个正三角形各边的中点相连得到第二个正三角形,依此类推,一共画了5个正三角形.那么这五个正三角形的面积之和等于( )| A. | 2$\sqrt{3}$ | B. | $\frac{21}{16}$$\sqrt{3}$ | C. | $\frac{85}{64}$$\sqrt{3}$ | D. | $\frac{341}{256}$$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
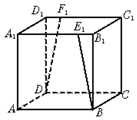 如图,ABCD-A1B1C1D1是正方体,${B_1}{E_1}={D_1}{F_1}=\frac{{{A_1}{B_1}}}{4}$,则BE1与DF1所成角的余弦值是$\frac{15}{17}$.
如图,ABCD-A1B1C1D1是正方体,${B_1}{E_1}={D_1}{F_1}=\frac{{{A_1}{B_1}}}{4}$,则BE1与DF1所成角的余弦值是$\frac{15}{17}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com