
| A. | 充分不必要 | B. | 必要不充分 | C. | 充要 | D. | 非充分非必要 |
分析 利用不等式的性质与解法分别化简命题甲、乙,即可判断出关系.
解答 解:由命题乙:$\frac{1}{b}<\frac{1}{a}<0$,可得:a<b<0.
命题甲:ab>b2,化为:b(a-b)>0,∴$\left\{\begin{array}{l}{b>0}\\{a-b>0}\end{array}\right.$,或$\left\{\begin{array}{l}{b<0}\\{a-b<0}\end{array}\right.$,解得a>b>0,或a<b<0.
∴甲是乙的必要不充分条件.
故选:B.
点评 本题考查了不等式的解法、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 若(a-2)(b-3)≠0,则a≠2或b≠3 | B. | 若(a-2)(b-3)≠0,则a≠2且b≠3 | ||
| C. | 若(a-2)(b-3)=0,则a≠2或b≠3 | D. | 若(a-2)(b-3)=0,则a≠2且b≠3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
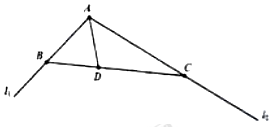 某市渭河的某水域有夹角为120°的两条直线河岸l1,l2(如图所示):在该水域中,位于该角平分线且距A地相距1公里的D处有座千年古亭,为保护古亭,沿D所在直线BC建一河堤(B,C分别在l1,l2上,河堤下方有进、出水的桥洞);现要在△ABC水域建一个水上游乐城,如何设计AB、AC河岸的长度,AB、AC都不超过5公里(不妨令AB=x公里,AC=y公里).
某市渭河的某水域有夹角为120°的两条直线河岸l1,l2(如图所示):在该水域中,位于该角平分线且距A地相距1公里的D处有座千年古亭,为保护古亭,沿D所在直线BC建一河堤(B,C分别在l1,l2上,河堤下方有进、出水的桥洞);现要在△ABC水域建一个水上游乐城,如何设计AB、AC河岸的长度,AB、AC都不超过5公里(不妨令AB=x公里,AC=y公里).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com