
分析 利用b2+c2-a2=bc,代入到余弦定理中求得cosA的值,进而求得A,再利用正弦定理求得b、c,利用两角和差的正弦公式化简b+c的解析式,结合正弦函数的定义域和值域,求得b+c 的范围.
解答 解:△ABC中,∵b2+c2-a2=bc,∴cosA=$\frac{{b}^{2}{+c}^{2}{-a}^{2}}{2bc}$=$\frac{1}{2}$,∴A=$\frac{π}{3}$,B+C=$\frac{2π}{3}$.
∵$\overrightarrow{AB}•\overrightarrow{BC}>0$,∴∠B为钝角.
∵$a=\frac{{\sqrt{3}}}{2}$,由正弦定理可得$\frac{a}{sinA}$=1=$\frac{b}{sinB}$=$\frac{c}{sinC}$,
∴b+c=sinB+sinC=sinB+sin($\frac{2π}{3}$-B)=sinB+$\frac{\sqrt{3}}{2}$cosB+$\frac{1}{2}$sinB
=$\frac{3}{2}$sinB+$\frac{\sqrt{3}}{2}$cosB=$\sqrt{3}$sin(B+$\frac{π}{6}$),
∵B∈($\frac{π}{2}$,$\frac{2π}{3}$),∴B+$\frac{π}{6}$∈($\frac{2π}{3}$,$\frac{5π}{6}$),∴sin(B+$\frac{π}{6}$)∈($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$),
∴b+c 的范围为$(\frac{{\sqrt{3}}}{2},\frac{3}{2})$,
故答案为:($\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).
点评 本题主要考查了余弦定理的应用.注意余弦定理的变形式的应用,考查计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 已知函数f(x)=x•|x|-2x.
已知函数f(x)=x•|x|-2x.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
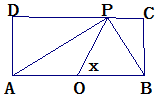 如图,长方形的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD,与DA运动,记∠BOP=x,将动点P到A,B两点距离之和表示为函数f(x),则f(x)的图象大致为( )
如图,长方形的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD,与DA运动,记∠BOP=x,将动点P到A,B两点距离之和表示为函数f(x),则f(x)的图象大致为( )| A. | 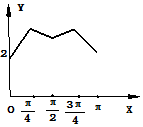 | B. | 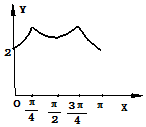 | ||
| C. | 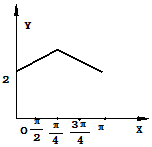 | D. | 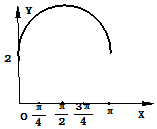 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图1,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于点A,将△PAD沿AD折起,构成如图2所示的四棱锥P-ABCD,点M的棱PB上,且PM=$\frac{1}{2}$MB.
如图1,在等腰梯形PDCB中,PB∥DC,PB=3,DC=1,∠DPB=45°,DA⊥PB于点A,将△PAD沿AD折起,构成如图2所示的四棱锥P-ABCD,点M的棱PB上,且PM=$\frac{1}{2}$MB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com