
分析 将圆C的方程整理为标准形式,找出圆心C的坐标与半径r,由题意可得以C为圆心,1为半径的圆与直线y=kx-1有公共点,即圆心到直线y=kx-1的距离小于等于1,利用点到直线的距离公式列出关于k的不等式求出不等式的解集,即可得到k的范围.
解答 解:将圆C的方程整理为标准方程得:(x+2)2+y2=1,∴圆心C(-2,0),半径r=1,
∵直线y=kx-1上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,
∴只需圆C:(x+2)2+y2=1与y=kx-1有公共点,
∵圆心(-2,0)到直线y=kx-1的距离d=$\frac{|-2k-1|}{\sqrt{{k}^{2}+1}}$≤1,求得-$\frac{4}{3}$≤k≤0,
故答案为:-$\frac{4}{3}$≤k≤0.
点评 此题考查了直线与圆的位置关系,涉及的知识有:圆的标准方程,点到直线的距离公式,其中当d<r时,直线与圆相交;当d>r时,直线与圆相离;当d=r时,直线与圆相切(d为圆心到直线的距离,r为圆的半径).


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
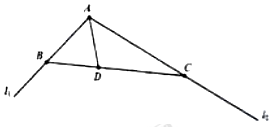 某市渭河的某水域有夹角为120°的两条直线河岸l1,l2(如图所示):在该水域中,位于该角平分线且距A地相距1公里的D处有座千年古亭,为保护古亭,沿D所在直线BC建一河堤(B,C分别在l1,l2上,河堤下方有进、出水的桥洞);现要在△ABC水域建一个水上游乐城,如何设计AB、AC河岸的长度,AB、AC都不超过5公里(不妨令AB=x公里,AC=y公里).
某市渭河的某水域有夹角为120°的两条直线河岸l1,l2(如图所示):在该水域中,位于该角平分线且距A地相距1公里的D处有座千年古亭,为保护古亭,沿D所在直线BC建一河堤(B,C分别在l1,l2上,河堤下方有进、出水的桥洞);现要在△ABC水域建一个水上游乐城,如何设计AB、AC河岸的长度,AB、AC都不超过5公里(不妨令AB=x公里,AC=y公里).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com