
| A. | $\frac{4}{3}π$ | B. | $\frac{8}{3}π$ | C. | $\frac{10}{3}π$ | D. | $\frac{16}{3}π$ |
分析 由题意,△ABC的外心是AC的中点O′,SO′⊥平面ABC,球心O在SO′上,利用勾股定理求出半径,即可求出四面体外接球的表面积.
解答 解:由题意,△ABC的外心是AC的中点O′,SO′⊥平面ABC,球心O在SO′上,设OO′=d,则($\sqrt{3}$-d)2=1+d2,
∴d=$\frac{\sqrt{3}}{3}$,r=$\sqrt{1+\frac{1}{3}}$=$\frac{2\sqrt{3}}{3}$,
∴该四面体外接球的表面积是$4π•\frac{4}{3}$=$\frac{16}{3}$π,
故选:D.
点评 本题考查四面体外接球的表面积,考查学生的计算能力,确定球心的位置是关键.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m≥1 | B. | m≥2 | C. | m≥3 | D. | m≥4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≤0或x≥2} | B. | {x|x<0或x>2} | C. | {x|x<-1或x>3} | D. | {x|x≤-1或x≥3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
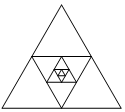 如图,画一个边长为2的正三角形,再将这个正三角形各边的中点相连得到第二个正三角形,依此类推,一共画了5个正三角形.那么这五个正三角形的面积之和等于( )
如图,画一个边长为2的正三角形,再将这个正三角形各边的中点相连得到第二个正三角形,依此类推,一共画了5个正三角形.那么这五个正三角形的面积之和等于( )| A. | 2$\sqrt{3}$ | B. | $\frac{21}{16}$$\sqrt{3}$ | C. | $\frac{85}{64}$$\sqrt{3}$ | D. | $\frac{341}{256}$$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
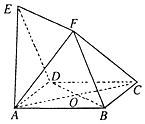 如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC,AC、BD交于点O.
如图,四边形ABCD与BDEF均为菱形,∠DAB=∠DBF=60°,且FA=FC,AC、BD交于点O.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com