
分析 根据正弦函数的性质求出f(x)的最小值及对应的x的值,利用导数判断g(x)的单调性,得出g(x)的最小值和对应的x,列出方程组即可得出b,c的值.
解答 解:令πx=$\frac{π}{2}$+2kπ得x=$\frac{1}{2}$+2k,k∈Z.
∴当x=$\frac{1}{2}$或x=$\frac{5}{2}$时,f(x)=-sin(πx)取得最小值-1.
g′(x)=3x2+b,
(1)若b≥0,则g′(x)≥0,
∴g(x)在[0,4]上是增函数,
∴当x=0时g(x)取得最小值,不符合题意;
(2)若b<0,令g′(x)=0得x=$\sqrt{-\frac{b}{3}}$或x=-$\sqrt{-\frac{b}{3}}$(舍).
①若$\sqrt{-\frac{b}{3}}$≥4,则g′(x)≤0,
∴g(x)在[0,4]上是减函数,
∴当x=4时g(x)取得最小值,不符合题意;
②若0<$\sqrt{-\frac{b}{3}}$<4,即-48<b<0时,
∴当0<x<$\sqrt{-\frac{b}{3}}$时,g′(x)<0,当$\sqrt{-\frac{b}{3}}$<x<4时,g′(x)>0,
∴g(x)在(0,$\sqrt{-\frac{b}{3}}$)上单调递减,在($\sqrt{-\frac{b}{3}}$,4)上单调递增,
∴当x=$\sqrt{-\frac{b}{3}}$时,g(x)取得最小值g($\sqrt{-\frac{b}{3}}$)=-$\frac{b}{3}$$\sqrt{-\frac{b}{3}}$+b$\sqrt{-\frac{b}{3}}$+c=$\frac{2b}{3}$$\sqrt{-\frac{b}{3}}$+c.
∴$\left\{\begin{array}{l}{\sqrt{-\frac{b}{3}}=\frac{1}{2}}\\{\frac{2b}{3}\sqrt{-\frac{b}{3}}+c=-1}\end{array}\right.$或$\left\{\begin{array}{l}{\sqrt{-\frac{b}{3}}=\frac{5}{2}}\\{\frac{2b}{3}\sqrt{-\frac{b}{3}}+c=-1}\end{array}\right.$.
解得b=c=-$\frac{3}{4}$或b=-$\frac{75}{4}$,c=$\frac{121}{4}$.
∴b-c=0或b-c=-49.
故答案为:0或-49.
点评 本题考查了导数与函数单调性的关系,函数最值的计算,正弦函数的性质,分类讨论思想,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
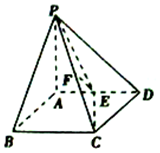 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,且PA=AD=2,BD=2$\sqrt{2}$,E、F分别为AD、PC中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为菱形,且PA=AD=2,BD=2$\sqrt{2}$,E、F分别为AD、PC中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
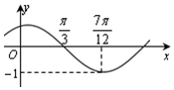 函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示,把函数f(x)的图象向右平移$\frac{π}{4}$个单位,得到函数y=g(x)的图象.
函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<$\frac{π}{2}$)的图象如图所示,把函数f(x)的图象向右平移$\frac{π}{4}$个单位,得到函数y=g(x)的图象.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com