
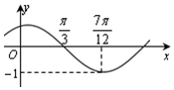
 ����f��x��=Asin����x+�գ�������A��0��|��|��$\frac{��}{2}$����ͼ����ͼ��ʾ���Ѻ���f��x����ͼ������ƽ��$\frac{��}{4}$����λ���õ�����y=g��x����ͼ��
����f��x��=Asin����x+�գ�������A��0��|��|��$\frac{��}{2}$����ͼ����ͼ��ʾ���Ѻ���f��x����ͼ������ƽ��$\frac{��}{4}$����λ���õ�����y=g��x����ͼ������ ��1����ͼ�����T���������ڹ�ʽ����أ���$2��\frac{��}{3}+ϕ=��$������գ���ͼ��任����y=g��x���ý���ʽ��
��2���ɺ���ͼ��ĶԳ��ԣ��������$g��{x_1}+{x_2}��=g��\frac{2��}{3}��=-\frac{1}{2}$��
��3��������ɵ�$sin��2C-\frac{��}{6}��=1$���ɷ�Χ0��C���У�����$-\frac{��}{6}��2C-\frac{��}{6}��\frac{11��}{6}$�����C��ֵ�����������߿���sinB-2sinA=0�������Ҷ��� $\frac{a}{sinA}=\frac{b}{sinB}$����b=2a�������Ҷ�������$9={a^2}+{b^2}-2abcos\frac{��}{3}$���������ɽ��a��b��ֵ��
��� ����������Ϊ12�֣�
�⣺��1���ɺ���f��x����ͼ��$T=4��\frac{7��}{12}-\frac{��}{3}��=\frac{2��}{��}$���æ�=2��
��$2��\frac{��}{3}+ϕ=��$��
�ɵã�$ϕ=\frac{��}{3}$��
����$f��x��=sin��2x+\frac{��}{3}��$������2�֣�
��ͼ��任����$g��x��=f��x-\frac{��}{4}��=sin��2x-\frac{��}{6}��$������4�֣�
��2���ɺ���ͼ��ĶԳ��ԣ���$g��{x_1}+{x_2}��=g��\frac{2��}{3}��=-\frac{1}{2}$������6�֣�
��3����$sin��2C-\frac{��}{6}��=1$��
��0��C����$-\frac{��}{6}��2C-\frac{��}{6}��\frac{11��}{6}$��
��$2C-\frac{��}{6}=\frac{��}{2}$��
��$C=\frac{��}{3}$�� ����7�֣�
��$\overrightarrow m��\overrightarrow n$���ߣ�
��sinB-2sinA=0��
�����Ҷ��� $\frac{a}{sinA}=\frac{b}{sinB}$����b=2a���١���9�֣�
��c=3�������Ҷ�������$9={a^2}+{b^2}-2abcos\frac{��}{3}$���ڡ���11�֣�
�ⷽ����٢ڣ���$\left\{\begin{array}{l}a=\sqrt{3}\\ b=2\sqrt{3}\end{array}\right.$�� ����12�֣�
���� ������Ҫ�������ɺ���y=Asin����x+�գ��IJ���ͼ�������ʽ�����Ǻ���ͼ��任���ɣ����Ǻ���ͼ��ĶԳ��ԣ����Ҷ��������Ҷ�����ƽ���������ߵ����ʵ�֪ʶ���ۺ�Ӧ�ã�������ת��˼�룬�����е��⣮


 ֱͨ������У�ܲ��¿�ֱͨ��Уϵ�д�
ֱͨ������У�ܲ��¿�ֱͨ��Уϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 24cm | B�� | 21cm | C�� | 19cm | D�� | 9cm |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{3\sqrt{2}}{2}$ | B�� | $\frac{\sqrt{14}}{2}$ | C�� | $\frac{3\sqrt{2}}{4}$ | D�� | $\frac{3\sqrt{2}}{2}$-1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��˵��ϣ���ϴ����˹��Pythagoras��Լ��Ԫǰ570��&��Ԫǰ500�꣩ѧ�ɵ���ѧ�Ҿ�����ɳ̲���о���ѧ���⣬������ɳ̲�ϻ������Сʯ������ʾ�������������ĸ�ͼ�μ���Ӧ�������εĸ����ı仯���ɣ���n��ͼ������$\frac{n��n+1��}{2}$�������Σ�
��˵��ϣ���ϴ����˹��Pythagoras��Լ��Ԫǰ570��&��Ԫǰ500�꣩ѧ�ɵ���ѧ�Ҿ�����ɳ̲���о���ѧ���⣬������ɳ̲�ϻ������Сʯ������ʾ�������������ĸ�ͼ�μ���Ӧ�������εĸ����ı仯���ɣ���n��ͼ������$\frac{n��n+1��}{2}$�������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
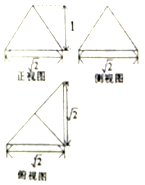
| A�� | $\frac{2}{3}$ | B�� | 1 | C�� | $\frac{1}{3}$ | D�� | 2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com