
【题目】如图,四棱锥P﹣ABCD的底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点. 
(1)证明PA∥平面BDE;
(2)证明:DE⊥面PBC;
(3)求直线AB与平面PBC所成角的大小.
【答案】
(1)证明:连结AC,设AC与BD交于O点,连结EO,
由O,E分别为AC,CP中点,
∴OE∥PA
又OE平面EDB,PA平面EDB,
∴PA∥平面EDB
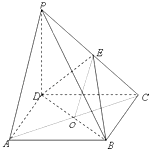
(2)证明:由PD⊥平面ABCD∴PD⊥BC又CD⊥BC,
∴BC⊥平面PCD,DE⊥BC.
由PD=DC,E为P中点,故DE⊥PC.
∴DE⊥平面PBC
(3)解:将几何体放到正方体中,则可得直线AB与平面PBC所成角的大小为45°
【解析】(1)连结AC,设AC与BD交于O点,连结EO,易证EO为△PAC的中位线,从而OE∥PA,再利用线面平行的判断定理即可证得PA∥平面BDE;(2)依题意,易证DE⊥底面PBC,再利用面面垂直的判断定理即可证得平面BDE⊥平面PBC;(3)将几何体放到正方体中,则可得直线AB与平面PBC所成角的大小.
【考点精析】根据题目的已知条件,利用直线与平面垂直的判定和空间角的异面直线所成的角的相关知识可以得到问题的答案,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则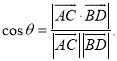 .
.


 天天练口算系列答案
天天练口算系列答案科目:高中数学 来源: 题型:
【题目】某居民小区内建有一块矩形草坪ABCD,AB=50米,![]() ,为了便于居民平时休闲散步,该小区物业管理公司将在这块草坪内铺设三条小路OE,EF和OF,考虑到小区整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且
,为了便于居民平时休闲散步,该小区物业管理公司将在这块草坪内铺设三条小路OE,EF和OF,考虑到小区整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且![]() ,如图所示.
,如图所示.

(Ⅰ)设![]() ,试将
,试将![]() 的周长l表示成
的周长l表示成![]() 的函数关系式,并求出此函数的定义域;
的函数关系式,并求出此函数的定义域;
(Ⅱ)经核算,三条路每米铺设费用均为400元,试问如何设计才能使铺路的总费用最低?并求出最低总费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合M={ ( x ,y ) | y=f(x) },若对于任意( x1 ,y1 )∈M,都存在( x2 ,y2 )∈M,使得x1 x2 +y1 y2 =0成立,则称集合M是“理想集合”,则下列集合是理想集合的是( )
A. M={ ( x ,y ) | y=![]() } B. M={ ( x ,y ) | y=log2 (x-1) }
} B. M={ ( x ,y ) | y=log2 (x-1) }
C. M={ ( x ,y ) | y=x2-2x+2 } D. M={ ( x ,y ) | y=cosx }
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,其中
,其中![]() 是实数.
是实数.
(l)若![]() ,求函数
,求函数![]() 的单调区间;
的单调区间;
(2)当![]() 时,若
时,若![]() 为函数
为函数![]() 图像上一点,且直线
图像上一点,且直线![]() 与
与![]() 相切于点
相切于点![]() ,其中
,其中![]() 为坐标原点,求
为坐标原点,求![]() 的值;
的值;
(3) 设定义在![]() 上的函数
上的函数![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,若
,若![]() 在定义域
在定义域![]() 内恒成立,则称函数
内恒成立,则称函数![]() 具有某种性质
具有某种性质![]() ,简称“
,简称“![]() 函数”.当
函数”.当![]() 时,试问函数
时,试问函数![]() 是否为“
是否为“![]() 函数”?若是,请求出此时切点
函数”?若是,请求出此时切点![]() 的横坐标;若不是,清说明理由.
的横坐标;若不是,清说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 定义域为
定义域为![]() ,若对于任意的
,若对于任意的![]() ,都有
,都有![]() ,且
,且![]() 时,有
时,有![]() .
.
(1)判断并证明函数![]() 的奇偶性;
的奇偶性;
(2)判断并证明函数![]() 的单调性;
的单调性;
(3)设![]() ,若
,若![]() ,对所有
,对所有![]() ,
,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com