练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在直三棱柱中，已知，，．

    （1）求异面直线与夹角的余弦值；

    （2）求二面角平面角的余弦值．

    【答案】（1），（2）．

    【解析】

    试题分析：（1）利用空间向量求线线角，关键在于正确表示各点的坐标. 以为正交基底，建立空间直角坐标系．则，，，，所以，,因此，所以异面直线与夹角的余弦值为．（2）利用空间向量求二面角，关键在于求出一个法向量. 设平面的法向量为，则 即取平面的一个法向量为；同理可得平面的一个法向量为；由两向量数量积可得二面角平面角的余弦值为．

    试题解析：

    如图，以为正交基底，建立空间直角坐标系．

    则，，，，所以，，

    ，．

    （1）因为，

    所以异面直线与夹角的余弦值为． 4分

    （2）设平面的法向量为，

    则 即

    取平面的一个法向量为；

    所以二面角平面角的余弦值为． 10分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】公差不为0的等差数列中，已知且，其前项和的最大值为（ ）

    A. 25 B. 26 C. 27 D. 28

    【答案】B

    【解析】设等差数列的公差为,

    ∵，

    ∴，

    整理得，

    ∵，

    ∴．

    ∴，

    ∴当时， ．

    故最大，且．选B．

    点睛：求等差数列前n项和最值的常用方法：

    ①利用等差数列的单调性， 求出其正负转折项，便可求得和的最值；

    ②将等差数列的前n项和 (A、B为常数)看作关于n的二次函数，根据二次函数的性质求最值．

    【题型】单选题
    【结束】
    9

    【题目】如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的表面积为（ ）

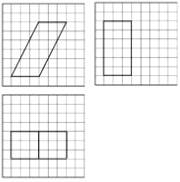
    A. B. C. 90 D. 81

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设为实数，设函数，设

    ．

    （1）求的取值范围，并把表示为的函数；

    （2）若恒成立，求实数的取值范围；

    （3）若存在使得成立，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设函数满足

    （1）求的值；

    （2）判断函数的奇偶性，并说明理由；

    （3）若b=1，且函数在上是单调增函数，求a的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列结论：

    ①y＝πx是指数函数

    ②函数既是偶函数又是奇函数

    ③函数的单调递减区间是

    ④在增函数与减函数的定义中，可以把任意两个自变量”改为“存在两个自变量

    ⑤与表示同一个集合

    ⑥所有的单调函数都有最值

    其中正确命题的序号是_______________。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥P﹣ABCD的底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点．

    （1）证明PA∥平面BDE；
    （2）证明：DE⊥面PBC；
    （3）求直线AB与平面PBC所成角的大小．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C:.

    （1）若圆C的切线在x轴和y轴上的截距相等，且截距不为零，求此切线的方程；

    （2）从圆C外一点P向该圆引一条切线，切点为M，O为坐标原点，且有，

    求使得取得最小值的点P的坐标

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若关于的不等式恰好有4个整数解，则实数的取值范围是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某家庭进行理财投资，根据长期收益率市场预测，投资类产品的收益与投资额成正比，投资类产品的收益与投资额的算术平方根成正比．已知投资1万元时两类产品的收益分别为0．125万元和0．5万元．

    （1）分别写出两类产品的收益与投资额的函数关系；

    （2）该家庭有20万元资金，全部用于理财投资，问：怎么分配资金能使投资获得最大收益，其最大收益是多少万元？

    查看答案和解析>>

    同步练习册答案