
����Ŀ�����Ϊ0�ĵȲ�����![]() �У���֪
�У���֪![]() ��
��![]() ����ǰ
����ǰ![]() ���
���![]() �����ֵΪ�� ��
�����ֵΪ�� ��
A. 25 B. 26 C. 27 D. 28
���𰸡�B
����������Ȳ�����![]() �Ĺ���Ϊ
�Ĺ���Ϊ![]() ,
,
��![]() ��
��
��![]() ��
��
������![]() ��
��
��![]() ��
��
��![]() ��
��
��![]() ��
��
�൱![]() ʱ��
ʱ�� ![]() ��
��
��![]() �����
�����![]() ��ѡB��
��ѡB��
�㾦����Ȳ�����ǰn�����ֵ�ij��÷�����
�����õȲ����еĵ����ԣ� ���������ת�����������ú͵���ֵ��
�����Ȳ����е�ǰn���![]() (A��BΪ����)��������n�Ķ��κ��������ݶ��κ�������������ֵ��
(A��BΪ����)��������n�Ķ��κ��������ݶ��κ�������������ֵ��
�����͡���ѡ��
��������
9
����Ŀ����ͼ������ֽ��С�����εı߳�Ϊ1����ʵ��������ij�����������ͼ����ö�����ı����Ϊ�� ��
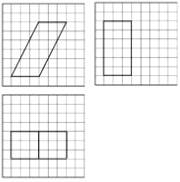
A. ![]() B.
B. ![]() C. 90 D. 81
C. 90 D. 81

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��һ�����ߣ��е�ΪB��ֱ��ADE��CFD��CGE���ǡ�O�ĸ��ߣ���֪AC=AB�� 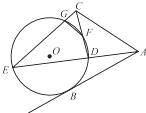
��1����CG=1��CD=4���� ![]() ��ֵ��
��ֵ��
��2����֤��FG��AC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��
��
��1����q=1ʱ����f��x����[��1��9]�ϵ�ֵ��
��2���ʣ��Ƿ���ڳ���q��0��q��10����ʹ�õ�x��[q��10]ʱ��f��x������СֵΪ��51�������ڣ����q��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������������У�
��1����֪���� ����
����![]() ��
��
��2����![]() ������ֱ��
������ֱ��![]() ��ֱ��
��ֱ��![]() ���ഹֱ���ı�Ҫ�����������
���ഹֱ���ı�Ҫ�����������
��3����֪�������![]() ������̬�ֲ�
������̬�ֲ�![]() ����
����![]() ����
����![]() ��
��
��4����֪Բ![]() ��Բ
��Բ![]() ����������Բǡ������������.
����������Բǡ������������.
����������ĸ���Ϊ
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����12�֣���֪����f��x��=![]()
��1���жϺ���������[1,+�����ϵĵ�����,���ö���֤����Ľ��ۣ�
��2����ú���������[1,4]�ϵ����ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�
�У� ![]() ���Եı߷ֱ�Ϊ
���Եı߷ֱ�Ϊ![]() ����
����![]() .
.
(1)���![]() �Ĵ�С��
�Ĵ�С��
(2)��![]() ��
�� ![]() ��
�� ![]() Ϊ
Ϊ![]() ���е㣬��
���е㣬��![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����˾����һ�ֵ��������Ĺ̶��ɱ�Ϊ20000Ԫ��ÿ����һ̨����������Ͷ��100Ԫ����֪���������㺯����
����  x ���������²���.
x ���������²���.
��1��������![]() ��ʾΪ�²���
��ʾΪ�²��� 
![]() �����
�����
��2�����²��� 
![]() Ϊ��ֵʱ����˾�������������������Ƕ���Ԫ����������=�ܳɱ�+����
Ϊ��ֵʱ����˾�������������������Ƕ���Ԫ����������=�ܳɱ�+����![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() �������߾�����
�������߾�����![]()
��1�����ۺ���![]() �ĵ����ԣ�
�ĵ����ԣ�
��2��������ʽ![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
���𰸡���1��![]() ��
��![]() �����ݼ�;��2��
�����ݼ�;��2��![]()
���������������: (1)���õ�����������,������߷���,�������߹���![]() ,�������
,�������![]() �Ľ���ʽ; (2)����֪����ʽ�����
�Ľ���ʽ; (2)����֪����ʽ�����![]() ,��
,�� ,��
,��![]() ,�ó�
,�ó�![]() ��
��![]() ��������,�����
��Ϊ������,����� ����Сֵ,�Ӷ��ó�
����Сֵ,�Ӷ��ó�![]() �ķ�Χ.
�ķ�Χ.
�������:��1��![]()
��![]() ��
��![]()
��![]() ���е�Ϊ
���е�Ϊ![]()
![]() ����
����![]()
![]() ��
��![]()
��![]()
��![]() ��
��![]() �����ݼ�
�����ݼ�
��2��![]() �����
�����

��![]()
![]()
��![]() ��
��![]() �����ݼ�
�����ݼ�
��![]()
��
��![]() ��
��![]() �����0
�����0
��![]()
�㾦: ������Ҫ�����˵����ļ��������Լ�������Ӧ��,���������ĵ����Ժ���ֵ,�����е���. ע��ڶ����еĺ��������,�ȼ�ת��Ϊ�� ����Сֵ,ֱ����
����Сֵ,ֱ���� ����Сֵ�Ƚϸ���,��������
����Сֵ�Ƚϸ���,��������![]() ,�����
,�����![]() �ϵĵ�����,�����
�ϵĵ�����,����� ����Сֵ,�õ�
����Сֵ,�õ�![]() �ķ�Χ.
�ķ�Χ.
�����͡������
��������
22
����Ŀ����֪![]() ����Բ
����Բ![]() ���������㣬
���������㣬 ![]() Ϊ����ԭ�㣬Բ
Ϊ����ԭ�㣬Բ![]() ����
����![]() Ϊֱ����Բ��һֱ��
Ϊֱ����Բ��һֱ��![]() ��Բ
��Բ![]() ���в�����Բ���ڲ�ͬ������
���в�����Բ���ڲ�ͬ������![]() .
.
��1����![]() ��
��![]() ��ϵʽ��
��ϵʽ��
��2����![]() ����ֱ��
����ֱ��![]() �ķ��̣�
�ķ��̣�
��3����![]() ��������
��������![]() ʱ����
ʱ����![]() �����ȡֵ��Χ.
�����ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ������![]() �У���֪
�У���֪![]() ��
��![]() ��
��![]() ��
��

��1��������ֱ��![]() ��
��![]() �нǵ�����ֵ��
�нǵ�����ֵ��
��2��������![]() ƽ��ǵ�����ֵ��
ƽ��ǵ�����ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com