
【题目】已知函数![]() ,其中a,
,其中a,![]() .
.
(I)若直线![]() 是曲线
是曲线![]() 的切线,求ab的最大值;
的切线,求ab的最大值;
(Ⅱ)设![]() ,若关于x的方程
,若关于x的方程![]() 有两个不相等的实根,求a的最大整数值.(参考数据:
有两个不相等的实根,求a的最大整数值.(参考数据:![]() )
)
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]()
【解析】
(I)设出直线![]() 与
与![]() 相切的切点坐标为
相切的切点坐标为![]() ,然后对函数进行求导,这样可以得到
,然后对函数进行求导,这样可以得到![]() ,切点又在直线
,切点又在直线![]() 上,这样可以得到
上,这样可以得到
![]() ,则有
,则有![]() ,设函数
,设函数
![]() ,求导,判断函数
,求导,判断函数![]() 的单调性,最后求出函数
的单调性,最后求出函数![]() 的最大值,也就求出ab的最大值;
的最大值,也就求出ab的最大值;
(Ⅱ)方法1:原方程化为![]() ,令
,令![]() 进行换元,方程等价于
进行换元,方程等价于![]() ,构造函数
,构造函数![]() ,原问题等价于函数
,原问题等价于函数![]() 需有两个不同的零点.对函数
需有两个不同的零点.对函数![]() 进行求导,根据函数
进行求导,根据函数![]() 的导函数的单调性,可以知道
的导函数的单调性,可以知道![]() 在
在![]() 上存在唯一实根
上存在唯一实根![]() ,这样可以判断出函数
,这样可以判断出函数![]() 的单调性,然后根据
的单调性,然后根据![]() 的正负性进行分类讨论,根据函数的单调性最后求出a的最大整数值.
的正负性进行分类讨论,根据函数的单调性最后求出a的最大整数值.
方法2:原方程即为![]() ,设
,设![]() ,
,
则原方程等价于关于![]() 的方程
的方程![]() 有两个不同的解,
有两个不同的解,
即关于![]() 的方程
的方程![]() )有两个不同的解.构造函数
)有两个不同的解.构造函数![]() ,求导得,得到函数的单调性,最后求出a的最大整数值.,
,求导得,得到函数的单调性,最后求出a的最大整数值.,
解:(I)设直线![]() 与
与![]() 相切于点
相切于点![]() .
.
因为![]() ,所以
,所以![]()
所以![]() .
.
又因为P在切线![]() 上,所以
上,所以![]()
所以![]() ,
,![]() ,
,
因此![]() .
.
设![]() ,
,
则由![]()
解得![]() .
.
所以![]() 在
在 上单调递增,在
上单调递增,在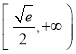 上单调递减,
上单调递减,
可知![]() 的最大值为
的最大值为 ,
,
所以![]() 的最大值为
的最大值为![]() .
.
(Ⅱ)方法1:原方程即为![]() ,
,
设![]() ,则上述方程等价于
,则上述方程等价于![]() .
.
设![]() ,则函数
,则函数![]() 需有两个不同的零点.
需有两个不同的零点.
因为![]() 在
在![]() 上单调递减,
上单调递减,
且![]() 在
在![]() 上存在唯一实根
上存在唯一实根![]() ,
,
即![]() ,即
,即![]() .
.
所以当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() .
.
因此![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
若![]() ,则
,则![]() .
.
![]() ,
,
不合题意,舍去.
若![]() ,则
,则![]() .
.
当![]() 时,则
时,则![]() ,
,
取![]() ,则
,则![]() ;
;
当![]() 时,则
时,则![]() ,
,
取![]() ,则
,则![]() .
.
由此![]() ,且
,且![]() ,
,![]() .
.
要使函数![]() 有两个不同的零点,
有两个不同的零点,
则只需![]() ,
,
所以只需![]() .
.
因为![]() 是关于
是关于![]() 的增函数.
的增函数.
且![]() ,
,![]()
所以存在![]() 使得
使得![]() ,
,
所以当![]() 时,
时,![]() .
.
因为![]() 是关于
是关于![]() 的减函数,
的减函数,
所以![]()
又因为![]() ,
,
所以![]() 的最大整数值为
的最大整数值为![]() .
.
方法2:原方程即为![]() ,设
,设![]() ,
,
则原方程等价于关于![]() 的方程
的方程![]() 有两个不同的解,
有两个不同的解,
即关于![]() 的方程
的方程![]() )有两个不同的解.
)有两个不同的解.
设![]() ,则
,则![]() .
.
设![]() ,
,
由![]() 知
知![]() ,所以
,所以![]()
在区间![]() 上单调递减,又
上单调递减,又![]() ,
,
所以存在![]() 使得
使得![]() .
.
当![]() 时,
时,![]() ,
,![]() ;当
;当![]() 时,
时,![]() ,
,![]() .
.
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所照![]() .
.
要使得关于![]() 的方程
的方程![]() 有两个不同的解,则
有两个不同的解,则![]() .
.
当![]() 时,设
时,设![]() ,
,
则![]() ,可知
,可知![]() 在
在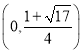 上单调递增,
上单调递增,
在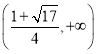 单调递减.
单调递减.
又![]() ,
,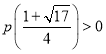 ,
,![]() ,
,
![]() 有两个不同的零点,符合题意.
有两个不同的零点,符合题意.
所以![]() 的最大整数值为
的最大整数值为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,已知平面![]()
![]() 平面
平面![]() ,
, ![]() 与
与![]() 分别是棱长为1与2的正三角形,
分别是棱长为1与2的正三角形, ![]() //
// ![]() ,四边形
,四边形![]() 为直角梯形,
为直角梯形, ![]() //
// ![]() ,
, ![]() ,点
,点![]() 为
为![]() 的重心,
的重心, ![]() 为
为![]() 中点,
中点, ![]() .
.

(Ⅰ)当![]() 时,求证:
时,求证: ![]() //平面
//平面![]() ;
;
(Ⅱ)若直线![]() 与
与![]() 所成角为
所成角为![]() ,试求二面角
,试求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出命题:(1)对立事件一定是互斥事件.(2)若事件![]() 满足
满足![]() ,则
,则![]() 为对立事件.(3)把
为对立事件.(3)把![]() 、
、![]() 、
、![]() ,3张红桃牌随机分给甲、乙、丙三人,每人1张,事件
,3张红桃牌随机分给甲、乙、丙三人,每人1张,事件![]() :“甲得红桃
:“甲得红桃![]() ”与事件
”与事件![]() :“乙得红桃
:“乙得红桃![]() ”是对立事件.(4)一个人打靶时连续射击两次,事件“至少有一次中靶”的对立事件是两次都不中靶.其中正确的命题个数为( )
”是对立事件.(4)一个人打靶时连续射击两次,事件“至少有一次中靶”的对立事件是两次都不中靶.其中正确的命题个数为( )
A.4B.3C.2D.1
查看答案和解析>>
科目:高中数学 来源: 题型:
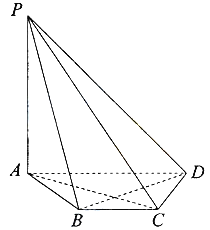
【题目】如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是等腰梯形,AD∥BC,AC⊥BD.
(Ⅰ)证明:BD⊥PC;
(Ⅱ)若AD=4,BC=2,直线PD与平面PAC所成的角为30°,求四棱锥P-ABCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 是公差为2的等差数列,且
是公差为2的等差数列,且![]() 成等比数列.数列
成等比数列.数列![]() 满足:
满足:![]() ,
,![]() .
.
(Ⅰ)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(Ⅱ)设数列![]() 的前n项和为
的前n项和为![]() ,且
,且 ,若对
,若对![]() ,
,![]() 恒成立,求正整数k的值.
恒成立,求正整数k的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司结合公司的实际情况针对调休安排展开问卷调查,提出了A,B,C三种放假方案,调查结果如下:

(1)在所有参与调查的人中,用分层抽样的方法抽取n个人,已知从“支持A方案”的人中抽取了6人,求n的值;
(2)在“支持B方案”的人中,用分层抽样的方法抽取5人看作一个总体,从这5人中任意选取2人,求恰好有1人在35岁以上(含35岁)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学团委组织了“纪念抗日战争胜利73周年”的知识竞赛,从参加竞赛的学生中抽出60名学生,将其成绩(均为整数)分成六段![]() ,
,![]() ,…,
,…,![]() 后,画出如图所示的部分频率分布直方图.观察图形给出的信息,回答下列问题:
后,画出如图所示的部分频率分布直方图.观察图形给出的信息,回答下列问题:
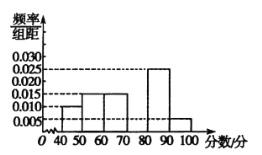
(1)求第四组的频率,并补全这个频率分布直方图;
(2)估计这次竞赛的及格率(60分及以上为及格)和平均分(同一组中的数据用该组区间的中点值代表)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某音乐院校举行“校园之星”评选活动,评委由本校全体学生组成,对![]() 两位选手,随机调查了
两位选手,随机调查了![]() 个学生的评分,得到下面的茎叶图:
个学生的评分,得到下面的茎叶图:
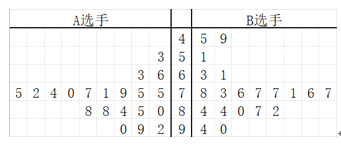
![]() 通过茎叶图比较
通过茎叶图比较![]() 两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
两位选手所得分数的平均值及分散程度(不要求计算出具体值,得出结论即可);
![]() 校方将会根据评分记过对参赛选手进行三向分流:
校方将会根据评分记过对参赛选手进行三向分流:
所得分数 | 低于 |
| 不低于 |
分流方向 | 淘汰出局 | 复赛待选 | 直接晋级 |
记事件![]() “
“![]() 获得的分流等级高于
获得的分流等级高于![]() ”,根据所给数据,以事件发生的频率作为相应事件发生的概率,求事件
”,根据所给数据,以事件发生的频率作为相应事件发生的概率,求事件![]() 发生的概率.
发生的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com