
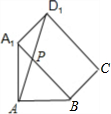
 如图,棱长为1的正方体ABCD-A1B1C1D1中,P为线段A1B上的动点,则下列结论错误的是( )
如图,棱长为1的正方体ABCD-A1B1C1D1中,P为线段A1B上的动点,则下列结论错误的是( )| A、DC1⊥D1P | ||||
| B、平面D1A1P⊥平面A1AP | ||||
| C、∠APD1的最大值为90° | ||||
D、AP+PD1的最小值为
|
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
2+
|


科目:高中数学 来源: 题型:
| A、S4>T4 |
| B、S4<T4 |
| C、S4=T4 |
| D、S4≤T4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、若m∥α,α∩β=n,则m∥n |
| B、若m⊥α,n⊥β,α⊥β,则m⊥n |
| C、若α⊥β,α∩β=n,m⊥n,则m⊥β |
| D、若m⊥α,m⊥n,则n∥α |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
 |
| y |
| A、65.5百万元 |
| B、72.0百万元 |
| C、82.5百万元 |
| D、83.0百万元 |
查看答案和解析>>
科目:高中数学 来源:2015届四川省成都市新都区高三诊断测试理科数学试卷(解析版) 题型:解答题
已知函数f(x)=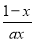 +lnx.
+lnx.
(1)若函数f(x)在[1,+∞)上为增函数,求实数a的取值范围;
(2)设数列{bn}的前n项和为Sn,其中bn=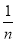 ,求证:当n≥2时,1+lnn>Sn.
,求证:当n≥2时,1+lnn>Sn.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com