
【题目】已知函数![]()
![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() ,记
,记![]() ,
,![]() ;
;
(1)求实数![]() 、
、![]() 的值;
的值;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的范围;
的范围;
(3)对于定义在![]() 上的函数
上的函数![]() ,设
,设![]() ,
,![]() ,用任意
,用任意![]()
![]() 将
将![]() 划分成
划分成![]() 个小区间,其中
个小区间,其中![]() ,若存在一个常数
,若存在一个常数![]() ,使得不等式
,使得不等式![]() 恒成立,则称函数
恒成立,则称函数![]() 为在
为在![]() 上的有界变差函数,试证明函数
上的有界变差函数,试证明函数![]() 是在
是在![]() 上的有界变差函数,并求出
上的有界变差函数,并求出![]() 的最小值;
的最小值;
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)证明见解析,
;(3)证明见解析,![]() ;
;
【解析】
(1)由已知![]() 在区间
在区间![]() 上的最大值为4,最小值为1,结合函数的单调性及最值,易构造关于
上的最大值为4,最小值为1,结合函数的单调性及最值,易构造关于![]() 的方程组,解得
的方程组,解得![]() 的值。
的值。
(2)求出![]() ,
,![]() 对任意
对任意![]() 恒成立等价于
恒成立等价于![]() 恒成立,求实数
恒成立,求实数![]() 的范围。
的范围。
(3)根据有界变差函数的定义,我们先将区间![]() 进行划分,进而判断
进行划分,进而判断![]() 是否恒成立,进而得到结论。
是否恒成立,进而得到结论。
(1)因为![]() ,因为
,因为![]() ,对称轴
,对称轴![]()
所以![]() 在区间
在区间![]() 上是增函数,
上是增函数,
又函数![]()
![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]()
所以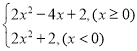
解得:![]()
所以![]()
故实数![]()
(2)由(1)可知![]()
因为![]() ,所以
,所以![]()
因为![]() 对任意
对任意![]() 恒成立,
恒成立,
令![]()
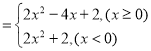
根据二次函数的图像和性质可得:![]()
则![]()
令![]() ,则
,则![]()
解得:![]()
即![]()
所以![]()
(3)函数![]() 为
为![]() 上的有界变差函数,又
上的有界变差函数,又![]() 为
为![]() 上的单增函数,
上的单增函数,
且对任意划分![]()
有![]()
所以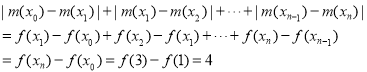
所以存在常数M使得![]() 恒成立,即
恒成立,即![]()


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)设点![]() 分别为曲线
分别为曲线![]() 与曲线
与曲线![]() 上的任意一点,求
上的任意一点,求![]() 的最大值;
的最大值;
(2)设直线![]() (
(![]() 为参数)与曲线
为参数)与曲线![]() 交于
交于![]() 两点,且
两点,且![]() ,求直线
,求直线![]() 的普通方程.
的普通方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】高铁是一种快捷的交通工具,为我们的出行提供了极大的方便。某高铁换乘站设有编号为①,②,③,④,⑤的五个安全出口,若同时开放其中的两个安全出口,疏散![]() 名乘客所需的时间如下:
名乘客所需的时间如下:
安全出口编号 | ①② | ②③ | ③④ | ④⑤ | ①⑤ |
疏散乘客时间(s) | 120 | 220 | 160 | 140 | 200 |
则疏散乘客最快的一个安全出口的编号是( )
A. ①B. ②C. ④D. ⑤
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xsinx的图象是下列两个图象中的一个,如图,请你选择后再根据图象作出下面的判断:若x1,x2∈(![]() ),且f(x1)<f(x2),则( )
),且f(x1)<f(x2),则( )
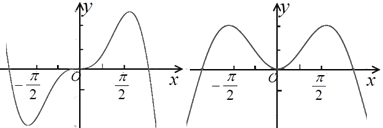
A.x1>x2B.x1+x2>0C.x1<x2D.x12<x22
查看答案和解析>>
科目:高中数学 来源: 题型:
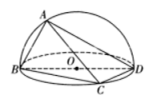
【题目】如图,已知![]() 是圆
是圆![]() 的直径,
的直径,![]() ,
,![]() 在圆上且分别在
在圆上且分别在![]() 的两侧,其中
的两侧,其中![]() ,
,![]() .现将其沿
.现将其沿![]() 折起使得二面角
折起使得二面角![]() 为直二面角,则下列说法不正确的是( )
为直二面角,则下列说法不正确的是( )
A.![]() ,
,![]() ,
,![]() ,
,![]() 在同一个球面上
在同一个球面上
B.当![]() 时,三棱锥
时,三棱锥![]() 的体积为
的体积为![]()
C.![]() 与
与![]() 是异面直线且不垂直
是异面直线且不垂直
D.存在一个位置,使得平面![]() 平面
平面![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,“大衍数列”:0,2,4,8,12….来源于《乾坤谱》中对《易传》“大衍之数五十”的推论,主要用于解释中国传统文化中的太极衍生过程中曾经经历过的两仪数量总和.下图是求大衍数列前![]() 项和的程序框图.执行该程序框图,输入
项和的程序框图.执行该程序框图,输入![]() ,则输出的
,则输出的![]() ( )
( )
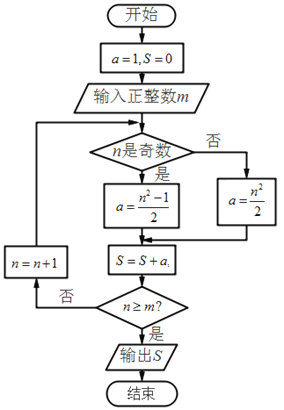
A.100B.140C.190D.250
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com