
【题目】已知函数f(x)=xsinx的图象是下列两个图象中的一个,如图,请你选择后再根据图象作出下面的判断:若x1,x2∈(![]() ),且f(x1)<f(x2),则( )
),且f(x1)<f(x2),则( )
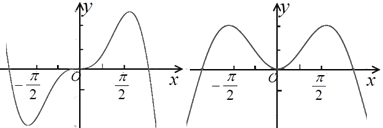
A.x1>x2B.x1+x2>0C.x1<x2D.x12<x22
【答案】D
【解析】
根据函数的解析式f(x)=xsinx,结合奇偶函数的判定方法得出函数f(x)=xsinx是偶函数,其图象关于y轴对称,其图象是右边一个图.再利用正弦函数的性质得出当x![]() 时和当x
时和当x![]() 时,函数f(x)=xsinx的单调性,即可对几个选项进行判断.
时,函数f(x)=xsinx的单调性,即可对几个选项进行判断.
解:由于函数f(x)=xsinx,
∴f(﹣x)=﹣xsin(﹣x)=xsinx=f(x),
∴函数f(x)=xsinx是偶函数,其图象关于y轴对称,其图象是右边一个图.
且当x![]() 时,函数f(x)=xsinx是增函数,
时,函数f(x)=xsinx是增函数,
∵x1,x2∈(![]() ),函数f(x)=xsinx是偶函数,且f(x1)<f(x2),
),函数f(x)=xsinx是偶函数,且f(x1)<f(x2),
∴![]() ,又当x
,又当x![]() 时,函数f(x)=xsinx是增函数,
时,函数f(x)=xsinx是增函数,
∴![]() ,
,
即x12<x22
故选:D.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() 在区间
在区间![]() 上的最大值为
上的最大值为![]() ,最小值为
,最小值为![]() ,记
,记![]() ,
,![]() ;
;
(1)求实数![]() 、
、![]() 的值;
的值;
(2)若不等式![]() 对任意
对任意![]() 恒成立,求实数
恒成立,求实数![]() 的范围;
的范围;
(3)对于定义在![]() 上的函数
上的函数![]() ,设
,设![]() ,
,![]() ,用任意
,用任意![]()
![]() 将
将![]() 划分成
划分成![]() 个小区间,其中
个小区间,其中![]() ,若存在一个常数
,若存在一个常数![]() ,使得不等式
,使得不等式![]() 恒成立,则称函数
恒成立,则称函数![]() 为在
为在![]() 上的有界变差函数,试证明函数
上的有界变差函数,试证明函数![]() 是在
是在![]() 上的有界变差函数,并求出
上的有界变差函数,并求出![]() 的最小值;
的最小值;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=lnx![]() ,a∈R.
,a∈R.
(1)若x=2是函数f(x)的极值点,求曲线y=f(x)在点(1,f(1))处的切线方程;
(2)若x>1时,f(x)>0,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线E:y2=4x与圆M:(x![]() 3)2+y2=r2(r>0)相交于A,B,C,D四个点.
3)2+y2=r2(r>0)相交于A,B,C,D四个点.
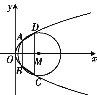
(1)求r的取值范围;
(2)设四边形ABCD的面积为S,当S最大时,求直线AD与直线BC的交点P的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 中心在原点,焦点在坐标轴上,直线
中心在原点,焦点在坐标轴上,直线![]() 与椭圆
与椭圆![]() 在第一象限内的交点是
在第一象限内的交点是![]() ,点
,点![]() 在
在![]() 轴上的射影恰好是椭圆
轴上的射影恰好是椭圆![]() 的右焦点
的右焦点![]() ,椭圆
,椭圆![]() 的另一个焦点是
的另一个焦点是![]() ,且
,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 过点
过点![]() ,且与椭圆
,且与椭圆![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的面积的最大值及此时
的面积的最大值及此时![]() 内切圆半径.
内切圆半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古印度“汉诺塔问题”:一块黄铜平板上装着![]() 三根金铜石细柱,其中细柱
三根金铜石细柱,其中细柱![]() 上套着个大小不等的环形金盘,大的在下、小的在上.将这些盘子全部转移到另一根柱子上,移动规则如下:一次只能将一个金盘从一根柱子转移到另外一根柱子上,不允许将较大盘子放在较小盘子上面.若
上套着个大小不等的环形金盘,大的在下、小的在上.将这些盘子全部转移到另一根柱子上,移动规则如下:一次只能将一个金盘从一根柱子转移到另外一根柱子上,不允许将较大盘子放在较小盘子上面.若![]() 柱上现有
柱上现有![]() 个金盘(如图),将
个金盘(如图),将![]() 柱上的金盘全部移到
柱上的金盘全部移到![]() 柱上,至少需要移动次数为( )
柱上,至少需要移动次数为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com