
【题目】已知椭圆![]() 中心在原点,焦点在坐标轴上,直线
中心在原点,焦点在坐标轴上,直线![]() 与椭圆
与椭圆![]() 在第一象限内的交点是
在第一象限内的交点是![]() ,点
,点![]() 在
在![]() 轴上的射影恰好是椭圆
轴上的射影恰好是椭圆![]() 的右焦点
的右焦点![]() ,椭圆
,椭圆![]() 的另一个焦点是
的另一个焦点是![]() ,且
,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 过点
过点![]() ,且与椭圆
,且与椭圆![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的面积的最大值及此时
的面积的最大值及此时![]() 内切圆半径.
内切圆半径.
【答案】(1)![]() ;(2)
;(2)![]() 的面积最大值为3,内切圆半径
的面积最大值为3,内切圆半径![]() .
.
【解析】
(1)由已知可得![]() ,根据
,根据![]() 可得
可得![]() ,将
,将![]() 代入椭圆可得
代入椭圆可得![]() ,从而可得
,从而可得![]() ,可得椭圆方程;
,可得椭圆方程;
(2)根据![]() 可得
可得![]()
![]() ,换元可得
,换元可得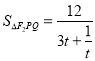 ,根据单调性可求得面积的最大值为3,根据
,根据单调性可求得面积的最大值为3,根据![]() (
(![]() 为三角形内切圆半径),可求得三角形内切圆半径.
为三角形内切圆半径),可求得三角形内切圆半径.
(1)设椭圆方程为![]() ,.点
,.点![]() 在直线
在直线![]() 上,且点
上,且点![]() 在
在![]() 轴上的射影恰好是椭圆
轴上的射影恰好是椭圆![]() 的右焦点
的右焦点![]() ,则点
,则点![]() .
.
∵![]() .即
.即![]() ,∴
,∴![]() ,所以
,所以![]() ,
,
又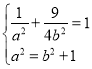 ,
,
解得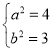 ,
,
∴椭圆方程为![]() .
.
(2)由(1)知![]() ,
,
设直线![]() 方程为
方程为![]() ,
,![]() ,
,![]() ,则
,则
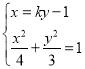 ,消去
,消去![]() 得
得![]() ,
,
∴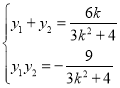 .
.
∴![]()
![]()
![]() ,
,
令![]() ,则
,则![]() ,∴
,∴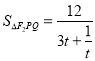 .
.
令![]() ,
,![]() ,
,
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,
上单调递增,
∴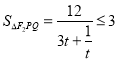 ,当
,当![]() 时取等号,
时取等号,
即当![]() 时,
时,![]() 的面积最大值为3.
的面积最大值为3.
过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,则
两点,则![]() 的周长为
的周长为![]() .
.
又![]() (
(![]() 为三角形内切圆半径),
为三角形内切圆半径),
∴当![]() 的面积最大时,
的面积最大时,![]() ,得内切圆半径
,得内切圆半径![]() .
.


 快乐5加2金卷系列答案
快乐5加2金卷系列答案科目:高中数学 来源: 题型:
【题目】某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图).已知上学所需时间的范围是![]() ,样本数据分组为
,样本数据分组为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(1)求直方图中x的值;
(2)如果上学所需时间在![]() 的学生可申请在学校住宿,请估计该校800名新生中有多少名学生可以申请住宿.
的学生可申请在学校住宿,请估计该校800名新生中有多少名学生可以申请住宿.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xsinx的图象是下列两个图象中的一个,如图,请你选择后再根据图象作出下面的判断:若x1,x2∈(![]() ),且f(x1)<f(x2),则( )
),且f(x1)<f(x2),则( )
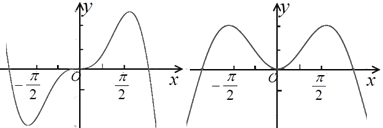
A.x1>x2B.x1+x2>0C.x1<x2D.x12<x22
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知正三棱锥P-ABC的侧面是直角三角形,PA=6,顶点P在平面ABC内的正投影为点D,D在平面PAB内的正投影为点E,连结PE并延长交AB于点G.

(Ⅰ)证明:G是AB的中点;
(Ⅱ)在图中作出点E在平面PAC内的正投影F(说明作法及理由),并求四面体PDEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,“大衍数列”:0,2,4,8,12….来源于《乾坤谱》中对《易传》“大衍之数五十”的推论,主要用于解释中国传统文化中的太极衍生过程中曾经经历过的两仪数量总和.下图是求大衍数列前![]() 项和的程序框图.执行该程序框图,输入
项和的程序框图.执行该程序框图,输入![]() ,则输出的
,则输出的![]() ( )
( )
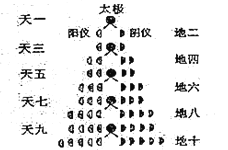
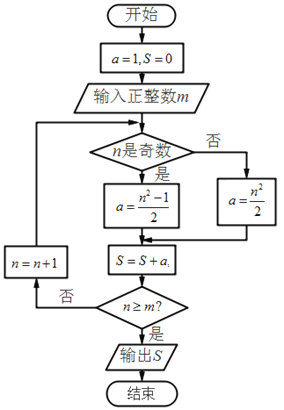
A.100B.140C.190D.250
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某学校研究性课题《什么样的活动最能促进同学们进行垃圾分类》向题的统计图(每个受访者都只能在问卷的5个活动中选择一个),以下结论错误的是( )

A. 回答该问卷的总人数不可能是100个
B. 回答该问卷的受访者中,选择“设置分类明确的垃圾桶”的人数最多
C. 回答该问卷的受访者中,选择“学校团委会宣传”的人数最少
D. 回答该问卷的受访者中,选择“公益广告”的人数比选择“学校要求”的少8个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 在椭圆
在椭圆![]() 上,
上,![]() 为坐标原点,直线
为坐标原点,直线![]() 的斜率与直线
的斜率与直线![]() 的斜率乘积为
的斜率乘积为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)不经过点![]() 的直线
的直线![]() (
(![]() 且
且![]() )与椭圆
)与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 关于原点的对称点为
关于原点的对称点为![]() (与点
(与点![]() 不重合),直线
不重合),直线![]() ,
,![]() 与
与![]() 轴分别交于两点
轴分别交于两点![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,
(1)求f(x)的单调递增区间;
(2)设△ABC的三个内角A,B,C的对边分别为a,b,c,若![]() 且a=2时,求△ABC周长的最大值.
且a=2时,求△ABC周长的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com