
【题目】已知函数![]() ,
,
(1)求f(x)的单调递增区间;
(2)设△ABC的三个内角A,B,C的对边分别为a,b,c,若![]() 且a=2时,求△ABC周长的最大值.
且a=2时,求△ABC周长的最大值.
【答案】(1)f(x)的单调递增区间:[kπ![]() ,kπ
,kπ![]() ],(k∈Z)(2)9
],(k∈Z)(2)9
【解析】
利用三角函数恒等变换的应用化简函数解析式可得![]() =sin(2x
=sin(2x![]() )
)![]() ,
,
(1)利用正弦函数的单调增区间和整体角思维,即可得解;
(2)根据题意,可求得![]() ,利用余弦定理和基本不等式求得
,利用余弦定理和基本不等式求得![]() 的最大值,进而求得三角形周长的最大值.
的最大值,进而求得三角形周长的最大值.
因为函数![]() sin2x=sin(2x
sin2x=sin(2x![]() )
)![]() ,
,
(1)令2kπ![]() 2x
2x![]() 2kπ
2kπ![]() kπ
kπ![]() x≤kπ
x≤kπ![]() ,(k∈Z);
,(k∈Z);
∴f(x)的单调递增区间:[kπ![]() ,kπ
,kπ![]() ],(k∈Z);
],(k∈Z);
(2)![]() sin(2A
sin(2A![]() )
)![]() sin(2A
sin(2A![]() )=1;
)=1;
∵0<A<π∴2A![]() A
A![]() ;
;
由余弦定理可知a2=b2+c2﹣2bccosA=b2+c2﹣bc=(b+c)2﹣3bc≥(b+c)2﹣3![]() ,
,
当且仅当b=c时等号成立.
于是b+c≤2a=6.故△ABC周长的最大值为9.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 中心在原点,焦点在坐标轴上,直线
中心在原点,焦点在坐标轴上,直线![]() 与椭圆
与椭圆![]() 在第一象限内的交点是
在第一象限内的交点是![]() ,点
,点![]() 在
在![]() 轴上的射影恰好是椭圆
轴上的射影恰好是椭圆![]() 的右焦点
的右焦点![]() ,椭圆
,椭圆![]() 的另一个焦点是
的另一个焦点是![]() ,且
,且![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 过点
过点![]() ,且与椭圆
,且与椭圆![]() 交于
交于![]() ,
,![]() 两点,求
两点,求![]() 的面积的最大值及此时
的面积的最大值及此时![]() 内切圆半径.
内切圆半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古印度“汉诺塔问题”:一块黄铜平板上装着![]() 三根金铜石细柱,其中细柱
三根金铜石细柱,其中细柱![]() 上套着个大小不等的环形金盘,大的在下、小的在上.将这些盘子全部转移到另一根柱子上,移动规则如下:一次只能将一个金盘从一根柱子转移到另外一根柱子上,不允许将较大盘子放在较小盘子上面.若
上套着个大小不等的环形金盘,大的在下、小的在上.将这些盘子全部转移到另一根柱子上,移动规则如下:一次只能将一个金盘从一根柱子转移到另外一根柱子上,不允许将较大盘子放在较小盘子上面.若![]() 柱上现有
柱上现有![]() 个金盘(如图),将
个金盘(如图),将![]() 柱上的金盘全部移到
柱上的金盘全部移到![]() 柱上,至少需要移动次数为( )
柱上,至少需要移动次数为( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在![]() 上的单调函数,且对任意的x∈
上的单调函数,且对任意的x∈![]() 都有
都有![]() ,则方程
,则方程![]() 的一个根所在的区间是( )
的一个根所在的区间是( )
A. (0,1) B. (1,2) C. (2,3) D. (3,4)
查看答案和解析>>
科目:高中数学 来源: 题型:
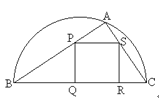
【题目】如图,某园林单位准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余的地方种花.若BC=a,∠ABC=![]() ,设△ABC的面积为S1,正方形的面积为S2.
,设△ABC的面积为S1,正方形的面积为S2.
(1)用a,![]() 表示S1和S2;
表示S1和S2;
(2)当a固定,![]() 变化时,求
变化时,求![]() 取最小值时的角
取最小值时的角![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com