
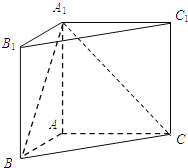
【题目】在直三棱柱![]() 中,
中,![]() ,且异面直线
,且异面直线![]() 与
与![]() 所成的角等于
所成的角等于![]() ,设
,设![]() .
.
(1)求![]() 的值;
的值;
(2)求直线![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)∠A1BC是异面直线A1B与B1C1所成的角,即∠A1BC=60°,根据线段的长度关系可得:△A1BC为等边三角形,即可得到![]() ,进而达到a=1.
,进而达到a=1.
(2)由B1C1∥平面A1BC,得点D到平面A1BC的距离等于点B1到平面A1BC的距离.再根据![]() 求B1到平面A1BC的距离,分别求出两个三角形的面积即可.
求B1到平面A1BC的距离,分别求出两个三角形的面积即可.
(1)∵BC∥B1C1,∴∠A1BC就是异面直线A1B与B1C1所成的角,
即∠A1BC=60°,又连接A1C,AB=AC,则A1B=A1C,∴△A1BC为等边三角形,
由AB=AC=1,∠BAC=90°,∴![]() ,∴
,∴![]() .
.
(2)易知B1C1∥平面A1BC,此时有B1C1上的任意一点到平面A1BC的距离等于点B1到平面A1BC的距离.
设其为d,连接B1C,由![]() 求d,又∵CA⊥A1A,CA⊥AB,
求d,又∵CA⊥A1A,CA⊥AB,
∴CA⊥平面A1B1C,并且AC=1,.因为△A1B1B的面积![]() ,并且△A1BC的面积
,并且△A1BC的面积![]() ,
,
所以![]() ,即
,即![]() ,所以B1C1到平面A1BC的距离等于
,所以B1C1到平面A1BC的距离等于![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,“大衍数列”:0,2,4,8,12….来源于《乾坤谱》中对《易传》“大衍之数五十”的推论,主要用于解释中国传统文化中的太极衍生过程中曾经经历过的两仪数量总和.下图是求大衍数列前![]() 项和的程序框图.执行该程序框图,输入
项和的程序框图.执行该程序框图,输入![]() ,则输出的
,则输出的![]() ( )
( )
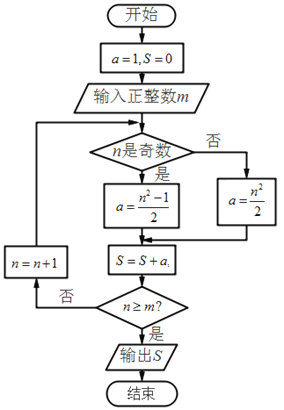
A.100B.140C.190D.250
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】互联网![]() 时代的今天,移动互联快速发展,智能手机
时代的今天,移动互联快速发展,智能手机![]() 技术不断成熟,价格却不断下降,成为了生活中必不可少的工具
技术不断成熟,价格却不断下降,成为了生活中必不可少的工具![]() 中学生是对新事物和新潮流反应最快的一个群体之一
中学生是对新事物和新潮流反应最快的一个群体之一![]() 逐渐地,越来越多的中学生开始在学校里使用手机
逐渐地,越来越多的中学生开始在学校里使用手机![]() 手机特别是智能手机在让我们的生活更便捷的同时会带来些问题,同学们为了解手机在中学生中的使用情况,对本校高二年级100名同学使用手机的情况进行调查
手机特别是智能手机在让我们的生活更便捷的同时会带来些问题,同学们为了解手机在中学生中的使用情况,对本校高二年级100名同学使用手机的情况进行调查![]() 针对调查中获得的“每天平均使用手机进行娱乐活动的时间”进行分组整理得到如图4的饼图、
针对调查中获得的“每天平均使用手机进行娱乐活动的时间”进行分组整理得到如图4的饼图、![]() 注:图中
注:图中![]() 2,
2,![]() 单位:小时
单位:小时![]() 代表分组为
代表分组为![]() i的情况
i的情况![]()

![]() 求饼图中a的值;
求饼图中a的值;
![]() 假设同一组中的每个数据可用给定区间的中点值代替,试估计样本中的100名学生每天平均使用手机的平均时间在第几组?
假设同一组中的每个数据可用给定区间的中点值代替,试估计样本中的100名学生每天平均使用手机的平均时间在第几组?![]() 只需写出结论
只需写出结论![]()
![]() 从该校随机选取一名同学,能否根据题目中所给信息估计出这名学生每天平均使用手机进行娱乐活动小于
从该校随机选取一名同学,能否根据题目中所给信息估计出这名学生每天平均使用手机进行娱乐活动小于![]() 小时的概率,若能,请算出这个概率;若不能,请说明理由
小时的概率,若能,请算出这个概率;若不能,请说明理由
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,
(1)求f(x)的单调递增区间;
(2)设△ABC的三个内角A,B,C的对边分别为a,b,c,若![]() 且a=2时,求△ABC周长的最大值.
且a=2时,求△ABC周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若各项为正实数的数列![]() 满足
满足![]() ,则称数列
,则称数列![]() 为“算术平方根递推数列”.
为“算术平方根递推数列”.
已知数列![]() 满足
满足![]() 且
且![]() 点
点![]() 在二次函数
在二次函数![]() 的图象上.
的图象上.
(1)试判断数列![]()
![]() 是否为算术平方根递推数列?若是,请说明你的理由;
是否为算术平方根递推数列?若是,请说明你的理由;
(2)记![]()
![]() ,求证:数列
,求证:数列![]() 是等比数列,并求出通项公式
是等比数列,并求出通项公式![]() ;
;
(3)从数列![]() 中依据某种顺序自左至右取出其中的项
中依据某种顺序自左至右取出其中的项![]() ,把这些项重新组成一个新数列
,把这些项重新组成一个新数列![]() :
:![]() .若数列
.若数列![]() 是首项为
是首项为![]() 、公比为
、公比为![]() 的无穷等比数列,且数列
的无穷等比数列,且数列![]() 各项的和为
各项的和为![]() ,求正整数
,求正整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中已知椭圆
中已知椭圆![]() 过点
过点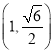 ,其左、右焦点分别为
,其左、右焦点分别为![]() ,离心率为
,离心率为![]() .
.
(1)求椭圆E的方程;
(2)若A,B分别为椭圆E的左、右顶点,动点M满足![]() ,且MA交椭圆E于点P.
,且MA交椭圆E于点P.
(i)求证:![]() 为定值;
为定值;
(ii)设PB与以PM为直径的圆的另一交点为Q,问:直线MQ是否过定点,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com