
【题目】如图,在![]() 中,
中,![]() ,且D为
,且D为![]() 的中点.
的中点.
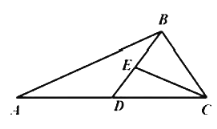
(1)求![]() 的值;
的值;
(2)若![]() ,
,![]() ,
,![]() 的角平分线
的角平分线![]() 交
交![]() 于E,求
于E,求![]() 及
及![]() 的面积.
的面积.
【答案】(1)![]() (2)
(2)![]() ,
,![]()
【解析】
(1)由D为AC的中点,可得S△ABC=2S△BCD,进而利用三角形的面积公式即可求解![]() 的值.
的值.
(2)设BD=x,则AB=2x,在△ABC,△BCD中,利用余弦定理可得![]() ,解得x2
,解得x2![]() ,可求cos∠DCB的值,利用角平分线的性质可求
,可求cos∠DCB的值,利用角平分线的性质可求![]() ,可得S△CED
,可得S△CED![]() S△BCD,利用三角形的面积公式求得S△BCD的值,即可求解S△CED的值.
S△BCD,利用三角形的面积公式求得S△BCD的值,即可求解S△CED的值.
解:(1)∵S△ABC![]() ABBCsin∠ABC,S△BCD
ABBCsin∠ABC,S△BCD![]() BDBCsin∠DBC,
BDBCsin∠DBC,
∵D为AC的中点,
∴S△ABC=2S△BCD,即![]() ABBCsin∠ABC=2
ABBCsin∠ABC=2![]() BDBCsin∠DBC,
BDBCsin∠DBC,
∵sin∠ABC=sin∠DBC,
∴![]() .
.
(2)设BD=x,则AB=2x,
在△ABC中,cos∠ACB![]() ,
,
在△BCD中,cos∠DCB![]() ,
,
∴![]() ,解得x2
,解得x2![]() ,则cos∠DCB
,则cos∠DCB![]() ,
,
∵∠ACB的角平分线为CE,
∴E到DC,BC的距离相等,则![]() ,
,
∴S△CED![]() S△BCD,
S△BCD,
∴S△BCD![]() BCDCsin∠DCB
BCDCsin∠DCB![]() 4
4![]() ,
,
∴S△CED![]() .
.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
【题目】己知函数y=f(x)在R上单调递增,函数y=f(x+1)的图象关于点(﹣1,0)对称,f(﹣1)=﹣2,则满足﹣2≤f(lgx﹣1)≤2的x的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为![]() .
.
(1)若a=1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为![]() ,求a.
,求a.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】几位大学生响应国家的创业号召,开发了![]() 三款软件,为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动,这三款软件的激活码分别为下面数学问题的三个答案:已知数列
三款软件,为激发大家学习数学的兴趣,他们推出了“解数学题获取软件激活码”的活动,这三款软件的激活码分别为下面数学问题的三个答案:已知数列![]() ,其中第一项是
,其中第一项是![]() ,接下来的两项是
,接下来的两项是![]() ,再接下来的三项是
,再接下来的三项是![]() ,以此类推,试根据下列条件求出三款软件的激活码
,以此类推,试根据下列条件求出三款软件的激活码
(1)A款应用软件的激活码是该数列中第四个三位数的项数的平方
(2)B款应用软件的激活码是该数列中第一个四位数及其前所有项的和
(3)C款应用软件的激活码是满足如下条件的最小整数![]() :①
:①![]() ;②该数列的前
;②该数列的前![]() 项和为2的整数幂
项和为2的整数幂
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某园林单位准备绿化一块直径为BC的半圆形空地,△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余的地方种花.若BC=a,∠ABC=![]() ,设△ABC的面积为S1,正方形的面积为S2.
,设△ABC的面积为S1,正方形的面积为S2.
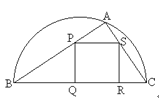
(1)用a,![]() 表示S1和S2;
表示S1和S2;
(2)当a固定,![]() 变化时,求
变化时,求![]() 取最小值时的角
取最小值时的角![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
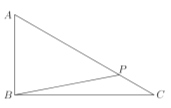
【题目】如图,某公园有三个警卫室![]() 、
、![]() 、
、![]() 有直道相连,
有直道相连,![]() 千米,
千米,![]() 千米,
千米,![]() 千米.
千米.
(1)保安甲沿![]() 从警卫室
从警卫室![]() 出发行至点
出发行至点![]() 处,此时
处,此时![]() ,求
,求![]() 的直线距离;
的直线距离;
(2)保安甲沿![]() 从警卫室
从警卫室![]() 出发前往警卫室
出发前往警卫室![]() ,同时保安乙沿
,同时保安乙沿![]() 从警卫室
从警卫室![]() 出发前往警卫室
出发前往警卫室![]() ,甲的速度为1千米/小时,乙的速度为2千米/小时,若甲乙两人通过对讲机联系,对讲机在公园内的最大通话距离不超过3千米,试问有多长时间两人不能通话?(精确到0.01小时)
,甲的速度为1千米/小时,乙的速度为2千米/小时,若甲乙两人通过对讲机联系,对讲机在公园内的最大通话距离不超过3千米,试问有多长时间两人不能通话?(精确到0.01小时)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的右焦点为
的右焦点为![]() ,过点
,过点![]() 的直线(不与
的直线(不与![]() 轴重合)与椭圆
轴重合)与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,直线
两点,直线![]() :
:![]() 与
与![]() 轴相交于点
轴相交于点![]() ,过点
,过点![]() 作
作![]() ,垂足为D.
,垂足为D.
(1)求四边形![]() (
(![]() 为坐标原点)面积的取值范围;
为坐标原点)面积的取值范围;
(2)证明直线![]() 过定点
过定点![]() ,并求出点
,并求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】 下列命题正确的个数是( )
①命题“x0∈R,![]() +1>3x0”的否定是“x∈R,x2+1≤3x”;
+1>3x0”的否定是“x∈R,x2+1≤3x”;
②“函数f(x)=cos2ax-sin2ax的最小正周期为π”是“a=1”的必要不充分条件;
③x2+2x≥ax在x∈[1,2]上恒成立(x2+2x)min≥(ax)max在x∈[1,2]上恒成立;
④“平面向量a与b的夹角是钝角”的充要条件是“a·b<0”.
A.1B.2
C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com