
分析 分别求出函数的定义域及值域判断(1)(2);由复合函数的单调性求出函数f(x)=$\sqrt{5+4x-{x}^{2}}$的单调递增区间判断(3);由正弦定理结合充分必要条件的判定方法判断(4).
解答 解:对于(1),函数y=ax(a>0且a≠1)的定义域为R,
函数函数y=logaax(a>0且a≠1)的定义域为R,故(1)正确;
对于(2),函数y=x3的值域为R,函数y=3x的值域为(0,+∞),故(2)错误;
对于(3),函数f(x)=$\sqrt{5+4x-{x}^{2}}$的单调递增区间为(-1,2],故(3)错误;
对于(4),在△ABC中,∠A>∠B?a>b,由正弦定理得a>b?sinA>sinB,
∴在△ABC中,∠A>∠B是sinA>sinB的充要条件,故(4)正确.
∴正确命题的序号是(1),(4).
故答案为:(1),(4).
点评 本题考查命题的真假判断与应用,考查了函数定义域及值域的求法,训练了充分必要条件的判定方法,是中档题.


科目:高中数学 来源: 题型:解答题
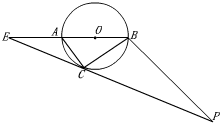 如图,圆O的直径AB=8,圆周上过点C的切线与BA的延长线交于点E,过点B作AC的平行线交EC的延长线于点P.
如图,圆O的直径AB=8,圆周上过点C的切线与BA的延长线交于点E,过点B作AC的平行线交EC的延长线于点P.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组数 | 分组 | 频数 | 频率 |
| 第一组 | [230,235) | 8 | 0.16 |
| 第二组 | [235,240) | p | 0.24 |
| 第三组 | [240,245) | 15 | q |
| 第四组 | [245,250) | 10 | 0.20 |
| 第五组 | [250,255] | 5 | 0.10 |
| 合计 | n | 1.00 | |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | -2 | D. | -1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com