|
|
|
在等腰梯形ABCD中,AB=3,AD=BC=2,CD=1,E为AB上的点且AE=1,将△AED沿DE折起到A1ED的位置,使得二面角A1-CD-E的平面角为30°.
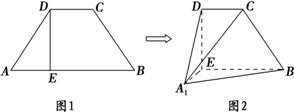
(1)求证:DE⊥A1B
(2)求二面角B-A1C-D的余弦值.
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设(2x-3)10=a0+a1(x-1)+a2(x-1)2+…+a10(x-1)10,则a1+a2+…+a10的值为________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
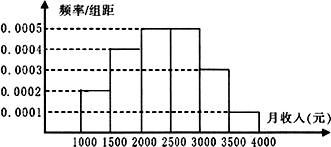
一个杜会调查机构就某地居民的月收人调查了10000人,并根据所得数据画出样本的频率分布直方图(如下图).为了分析居民的收人与年龄、学历、职业等方面的关系,按下图横轴表示的月收人情况分成六层,再从这10000人中用分层抽样的方法抽出100人作进一步调查,则在[2500,3000)(元)月收人层中应抽出的人数为________;
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若变量a,b满足约束条件 ,n=2a+3b,则n取最小值时, ,n=2a+3b,则n取最小值时, 二项展开式中的常数项为 二项展开式中的常数项为
|
| [ ] |
A. |
-80
|
B. |
80
|
C. |
40
|
D. |
-20
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
在极坐标系中,若等边三角形ABC(顶点A,B,C按顺时针方向排列)的顶点A,B的极坐标分别为 ,则顶点C的极坐标为________; ,则顶点C的极坐标为________;
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知等差数列{an}的前m项和为Sn,且S3=6,则5a1+a7,的值为
|
| [ ] |
A. |
12
|
B. |
10
|
C. |
24
|
D. |
6
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
过双曲线 的右焦点F和虚轴端点B(0,6)作一条直线,若右顶点A到直线FB的距离等于 的右焦点F和虚轴端点B(0,6)作一条直线,若右顶点A到直线FB的距离等于 ,则双曲线的离心率e= ,则双曲线的离心率e=
|
| [ ] |
A. |
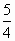
|
B. |
2
|
C. |
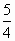 或2 或2
|
D. |
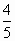
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
在同一平面直角坐标系下,下列曲线中,其右焦点与抛物线y2=4x的焦点重合的是
|
| [ ] |
A. |
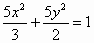
|
B. |
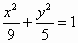
|
C. |
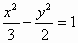
|
D. |
 =1 =1
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知椭圆 + + =1(a>b>0)的一个焦点F与抛物线y2=4x的焦点重合,且截抛物线的准线所得弦长为 =1(a>b>0)的一个焦点F与抛物线y2=4x的焦点重合,且截抛物线的准线所得弦长为 ,倾斜角为45°的直线l过点F. ,倾斜角为45°的直线l过点F.
(1)求该椭圆的方程;
(2)设椭圆的另一个焦点为F1,问抛物线y2=4x上是否存在一点M,使得M与F1关于直线l对称,若存在,求出点M的坐标,若不存在,说明理由.
|
|
|
查看答案和解析>>

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案