
| A. | 0 | B. | -2 | C. | -8 | D. | 8 |
分析 可判断函数f(x)的周期为2,从而化简可得f(x)-2=$\frac{1}{x}$,作函数f(x)-2与y=$\frac{1}{x}$在[-3,3]上的图象,从而结合图象解得.
解答 解:∵f(x+1)=f(x-1),
∴函数f(x)的周期为2,
∵f(x)=$\frac{2x+1}{x}$,
∴f(x)-2=$\frac{1}{x}$,
∵f(x)=$\left\{\begin{array}{l}{{x}^{2}+2,x∈[0,1]}\\{2-{x}^{2},x∈(-1,0)}\end{array}\right.$,
∴f(x)-2=$\left\{\begin{array}{l}{{x}^{2},x∈[0,1]}\\{{-x}^{2},x∈(-1,0)}\end{array}\right.$,
作函数y=f(x)-2与y=$\frac{1}{x}$在[-3,3]上的图象如下,
易知点A与点C关于原点对称,
故方程f(x)=$\frac{2x+1}{x}$在区间[-3,3]上的所有实根之和为0,
故选:A.
点评 本题考查了数形结合的思想应用及方程与函数的关系应用.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{6}{5}$ | D. | $\frac{8}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列说法,不正确的是( )
如图,边长为a的等边三角形ABC的中线AF与中位线DE交于点G,已知△A′DE(A′∉平面ABC)是△ADE绕DE旋转过程中的一个图形,有下列说法,不正确的是( )| A. | 平面A′FG⊥平面ABC | |
| B. | BC∥平面A′DE | |
| C. | 三棱锥A′-DEF的体积最大值为$\frac{1}{64}{a^3}$ | |
| D. | 直线DF与直线A′E有可能异面 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
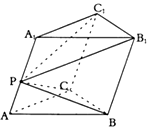 如图,P为三棱柱ABC-A1B1C1的侧棱AA1上的一个动点,若四棱锥P-BCC1B1的体积为V,则三棱柱ABC-A1B1C1的体积为$\frac{3}{2}V$(用V表示)
如图,P为三棱柱ABC-A1B1C1的侧棱AA1上的一个动点,若四棱锥P-BCC1B1的体积为V,则三棱柱ABC-A1B1C1的体积为$\frac{3}{2}V$(用V表示)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x∈R,x≤2 | B. | ¬p:?x∈R,x>2 | C. | ¬p:?x∈R,x>2 | D. | ¬p:?x∈R,x≤2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1<k<$\frac{\sqrt{5}}{2}$ | B. | -$\frac{\sqrt{5}}{2}$<k<$\frac{\sqrt{5}}{2}$ | C. | -$\frac{\sqrt{5}}{2}$<k<-1 | D. | -$\frac{\sqrt{5}}{2}$<k<1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
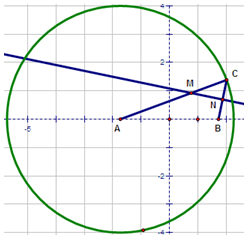 以$A(-\sqrt{3},0)$为圆心,4为半径作圆,$B(\sqrt{3},0)$,C为圆上任意一点,分别连接AC,BC,过BC的中点N作BC的垂线,交AC于点M,当点C在圆上运动时,
以$A(-\sqrt{3},0)$为圆心,4为半径作圆,$B(\sqrt{3},0)$,C为圆上任意一点,分别连接AC,BC,过BC的中点N作BC的垂线,交AC于点M,当点C在圆上运动时,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com