
【题目】正项数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(Ⅰ)试求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,求
,求![]() 的前
的前![]() 项和为
项和为![]() .
.
(Ⅲ)在(Ⅱ)的条件下,若![]() 对一切
对一切![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
(Ⅰ)将所给条件式子两边同时平方,利用递推法可得![]() 的表达式,由
的表达式,由![]() 两式相减,变形即可证明数列
两式相减,变形即可证明数列![]() 为等差数列,进而结合首项与公差求得
为等差数列,进而结合首项与公差求得![]() 的通项公式.
的通项公式.
(Ⅱ)由(Ⅰ)中![]() 可求得
可求得![]() .将
.将![]() 与
与![]() 代入
代入![]() 即可求得数列
即可求得数列![]() 的通项公式,利用裂项法即可求得前
的通项公式,利用裂项法即可求得前![]() 项和
项和![]() .
.
(Ⅲ)先求得![]() 的取值范围,结合不等式
的取值范围,结合不等式![]() ,即可求得
,即可求得![]() 的取值范围.
的取值范围.
(Ⅰ)因为正项数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]()
化简可得![]()
由递推公式可得![]()
两式相减可得![]() ,变形可得
,变形可得![]()
即![]() ,由正项等比数列可得
,由正项等比数列可得![]()
所以![]()
而当![]() 时,
时,![]() 解得
解得![]()
所以数列![]() 是以
是以![]() 为首项,以
为首项,以![]() 为公差的等差数列
为公差的等差数列
因而![]()
(Ⅱ)由(Ⅰ)可知![]()
则![]()
代入![]() 中可得
中可得![]()
所以![]()
![]()
![]()
![]()
(Ⅲ)由(Ⅱ)可知![]()
则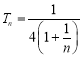 ,所以数列
,所以数列![]() 为单调递增数列,则
为单调递增数列,则![]()
且当![]() 时,
时, ![]() ,即
,即![]()
所以![]()
因为![]() 对一切
对一切![]() 的
的![]() 恒成立
恒成立
则满足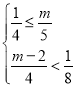 ,解不等式组可得
,解不等式组可得![]()
即实数![]() 的取值范围为
的取值范围为![]()


 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:
【题目】我国南宋数学家杨辉1261年所著的《详解九章算法》一书里出现了如图所示的表,即杨辉三角,这是数学史上的一个伟大成就,在“杨辉三角”中,第![]() 行的所有数字之和为
行的所有数字之和为![]() ,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列的前15项和为( )
,若去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列的前15项和为( )
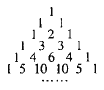
A. 110B. 114C. 124D. 125
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求使不等式
,求使不等式![]() 对一切
对一切![]() 都成立的正整数
都成立的正整数![]() 的最大值.
的最大值.
(3)设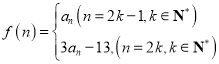 ,是否存在
,是否存在![]() ,使得
,使得![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】每年的金秋十月,越野e族阿拉善英雄会在内蒙古自治区阿拉善盟阿左旗腾格里沙漠举行,该项目已打造成集沙漠竞技运动、汽车文化极致体验、主题休闲度假为一体的超级汽车文化赛事娱乐综合体.为了减少对环境的污染,某环保部门租用了特制环保车清洁现场垃圾.通过查阅近5年英雄会参会人数![]() (万人)与沙漠中所需环保车辆数量
(万人)与沙漠中所需环保车辆数量![]() (辆),得到如下统计表:
(辆),得到如下统计表:
参会人数 | 11 | 9 | 8 | 10 | 12 |
所需环保车辆 | 28 | 23 | 20 | 25 | 29 |
(1)根据统计表所给5组数据,求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() .
.
(2)已知租用的环保车平均每辆的费用![]() (元)与数量
(元)与数量![]() (辆)的关系为
(辆)的关系为
![]() .主办方根据实际参会人数为所需要投入使用的环保车,
.主办方根据实际参会人数为所需要投入使用的环保车,
每辆支付费用6000元,超出实际需要的车辆,主办方不支付任何费用.预计本次英雄会大约有14万人参加,根据(Ⅰ)中求出的线性回归方程,预测环保部门在确保清洁任务完成的前提下,应租用多少辆环保车?获得的利润![]() 是多少?(注:利润
是多少?(注:利润![]() 主办方支付费用
主办方支付费用![]() 租用车辆的费用).
租用车辆的费用).
参考公式:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() ,
,![]() 是
是![]() 的中点,
的中点,![]() 是线段
是线段![]() 上异于端点的一点,平面
上异于端点的一点,平面![]()
![]() 平面
平面![]() ,
,![]() .
.

(Ⅰ)证明:![]() ;
;
(Ⅱ)若![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() ,求四棱锥
,求四棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列有关命题的说法正确的是___(请填写所有正确的命题序号).
①命题“若![]() ,则
,则![]() ”的否命题为:“若
”的否命题为:“若![]() ,则
,则![]() ”;
”;
②命题“若![]() ,则
,则![]() ”的逆否命题为真命题;
”的逆否命题为真命题;
③条件![]() ,条件
,条件![]() ,则
,则![]() 是
是![]() 的充分不必要条件;
的充分不必要条件;
④已知![]() 时,
时,![]() ,若
,若![]() 是锐角三角形,则
是锐角三角形,则![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com