
ЎҫМвДҝЎҝОӘәлСпГсЧеОД»ҜЈ¬ДіС§РЈС§ЙъИ«ФұІОУлҫЩРРБЛЎ°ОТ°®№ъС§Ј¬ҙ«ЛРҫӯөдЎұҝјКФЈ¬ІўҙУЦРійИЎ![]() ГыС§ЙъөДіЙјЁЈЁ°Щ·ЦЦЖЈ©ЧчОӘСщұҫЈ¬өГөҪЖөВК·ЦІјЦұ·ҪНјИзНјЛщКҫЈ®іЙјЁВдФЪ
ГыС§ЙъөДіЙјЁЈЁ°Щ·ЦЦЖЈ©ЧчОӘСщұҫЈ¬өГөҪЖөВК·ЦІјЦұ·ҪНјИзНјЛщКҫЈ®іЙјЁВдФЪ![]() ЦРөДИЛКэОӘ20Ј®
ЦРөДИЛКэОӘ20Ј®

ЈЁ1Ј©Зу![]() әН
әН![]() өДЦөЈ»
өДЦөЈ»
ЈЁ2Ј©ёщҫЭСщұҫ№АјЖЧЬМеөДЛјПлЈ¬№АјЖёГРЈС§ЙъКэС§іЙјЁөДЖҪҫщКэ![]() әНЦРО»Кэ
әНЦРО»Кэ![]() Ј»ЈЁН¬Т»ЧйКэҫЭЦРөДКэҫЭТФХвЧйКэҫЭЛщФЪЗшјдЦРөгөДЦөЧчҙъұнЈ©
Ј»ЈЁН¬Т»ЧйКэҫЭЦРөДКэҫЭТФХвЧйКэҫЭЛщФЪЗшјдЦРөгөДЦөЧчҙъұнЈ©
ЈЁ3Ј©ИфіЙјЁФЪ80·ЦТФЙПЈЁә¬80·ЦЈ©ОӘЎ°№ъѧСҙпИЛЎұЈ®ИфФЪСщұҫЦРЈ¬АыУГ·ЦІгійСщөД·Ҫ·ЁҙУЎ°№ъѧСҙпИЛЎұЦРЛж»ъійИЎ5ИЛЈ¬ФЩҙУЦРійИЎ2ИЛФщЛНТ»МЧ№ъС§ҫӯөдЈ¬јЗЎ°ійЦРөД2ГыС§ЙъіЙјЁ¶јІ»өНУЪ90·ЦЎұОӘКВјю![]() Ј¬Зу
Ј¬Зу![]() Ј»
Ј»
Ўҫҙр°ёЎҝЈЁ1Ј©![]() Ј¬
Ј¬![]() Ј» ЈЁ2Ј©ЖҪҫщКэОӘ
Ј» ЈЁ2Ј©ЖҪҫщКэОӘ![]() Ј¬ЦРО»КэОӘ
Ј¬ЦРО»КэОӘ![]() Ј» ЈЁ3Ј©
Ј» ЈЁ3Ј©![]() .
.
ЎҫҪвОцЎҝ
ЈЁ1Ј©УЙЖөВК·ЦІјЦұ·ҪНјөДРФЦКДЬЗуіц![]() Ј¬ФЩУЙіЙјЁВдФЪ
Ј¬ФЩУЙіЙјЁВдФЪ![]() Ј¬
Ј¬![]() ЦРөДЖөВКОӘ
ЦРөДЖөВКОӘ![]() Ј¬ДЬЗуіц
Ј¬ДЬЗуіц![]() Ј»
Ј»
ЈЁ2Ј©ёщҫЭСщұҫ№АјЖЧЬМеөДЛјПлЈ¬јҙҝЙ№АјЖёГРЈС§ЙъКэС§іЙјЁөДЖҪҫщКэәНЦРО»КэЈ»
ЈЁ3Ј©УЙ·ЦІгійСщҝЙЛгіцЈ¬іЙјЁФЪ![]() Ј¬
Ј¬![]() ЦРійИЎ3ИЛјЗОӘ
ЦРійИЎ3ИЛјЗОӘ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬Ј¬іЙјЁФЪ
Ј¬Ј¬іЙјЁФЪ![]() Ј¬
Ј¬![]() ЦРійИЎ2ИЛјЗОӘ
ЦРійИЎ2ИЛјЗОӘ![]() Ј¬
Ј¬![]() Ј¬АыУГБРҫЩ·ЁЈ¬Т»Т»БРіцҙУХв5ИЛЦРійИЎ2ИЛөДЛщУР»щұҫКВјюәНКВјюөД
Ј¬АыУГБРҫЩ·ЁЈ¬Т»Т»БРіцҙУХв5ИЛЦРійИЎ2ИЛөДЛщУР»щұҫКВјюәНКВјюөД![]() »щұҫКВјюЈ¬АыУГ№ЕөдёЕРНЗуёЕВКјҙҝЙЗуіц
»щұҫКВјюЈ¬АыУГ№ЕөдёЕРНЗуёЕВКјҙҝЙЗуіц![]() Ј®
Ј®
ҪвЈәЈЁ1Ј©УЙЖөВК·ЦІјЦұ·ҪНјЈ¬![]() Ј¬
Ј¬
Ўа![]() Ј¬
Ј¬
![]() ійИЎ
ійИЎ![]() ГыС§ЙъөДіЙјЁЈЁ°Щ·ЦЦЖЈ©ЧчОӘСщұҫЈ¬өГөҪЖөВК·ЦІјЦұ·ҪНјЈ¬
ГыС§ЙъөДіЙјЁЈЁ°Щ·ЦЦЖЈ©ЧчОӘСщұҫЈ¬өГөҪЖөВК·ЦІјЦұ·ҪНјЈ¬
іЙјЁВдФЪ![]() Ј¬
Ј¬![]() ЦРөДИЛКэОӘ20Ј¬
ЦРөДИЛКэОӘ20Ј¬
іЙјЁВдФЪ![]() Ј¬
Ј¬![]() ЦРөДЖөВКОӘ
ЦРөДЖөВКОӘ![]() Ј¬
Ј¬
Ўа![]() .
.
ЈЁ2Ј©УЙМвТвЈ¬ёчЧйөДЖөВК·ЦұрКЗ0.05Ј¬0.2Ј¬0.5Ј¬0.15Ј¬0.1Ј¬
Ўа![]() Ј¬
Ј¬
![]() Ј¬
Ј¬![]() өДЖөВКОӘ
өДЖөВКОӘ![]() Ј¬
Ј¬
![]() Ј¬
Ј¬![]() өДЖөВКОӘ
өДЖөВКОӘ![]() Ј¬
Ј¬
![]() ЦРО»Кэ
ЦРО»Кэ![]() Ј®
Ј®
ЈЁ3Ј©Ј©іЙјЁФЪ80·ЦТФЙПЈЁә¬80·ЦЈ©ОӘЎ°№ъѧСҙпИЛЎұЈ¬
ФЪСщұҫЦРЈ¬АыУГ·ЦІгійСщөД·Ҫ·ЁҙУЎ°№ъѧСҙпИЛЎұЦРЛж»ъійИЎ5ИЛЈ¬
ФтіЙјЁФЪ![]() Ј¬
Ј¬![]() ЦРійИЎ
ЦРійИЎ![]() ИЛЈ¬
ИЛЈ¬
іЙјЁФЪ![]() Ј¬
Ј¬![]() ЦРійИЎ
ЦРійИЎ![]() ИЛЈ¬
ИЛЈ¬
јЗіЙјЁФЪ![]() өД3ИЛОӘ
өД3ИЛОӘ![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬іЙјЁФЪ
Ј¬іЙјЁФЪ![]() өД2ИЛОӘ
өД2ИЛОӘ![]() Ј¬
Ј¬![]() Ј¬
Ј¬
ФтҙУХв5ИЛЦРійИЎ2ИЛөДЛщУРҝЙДЬҪб№ыУРЈә
![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬
Ј¬![]() Ј¬№І10ЦЦЈ®
Ј¬№І10ЦЦЈ®
ЖдЦРКВјю![]() Лщ°ьә¬өДҪб№ыУР
Лщ°ьә¬өДҪб№ыУР![]() Ј¬1ЦЦҪб№ыЈ¬
Ј¬1ЦЦҪб№ыЈ¬
УЙ№ЕөдёЕРНЗуёЕВК№«КҪөГЈә![]() Ј®
Ј®


 ГҝИХ10·ЦЦУҝЪЛгРДЛгЛЩЛгМмМмБ·ПөБРҙр°ё
ГҝИХ10·ЦЦУҝЪЛгРДЛгЛЩЛгМмМмБ·ПөБРҙр°ё
| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝҪ»ЗҝПХКЗіөЦчұШРлОӘ»ъ¶Ҝіө№әВтөДПХЦЦЈ¬ИфЖХНЁ6ЧщТФПВЛҪјТіөН¶ұЈҪ»ЗҝПХөЪТ»ДкөД·СУГ(»щЧјұЈ·С)НіТ»ОӘaФӘЈ¬ФЪПВТ»ДкРшұЈКұЈ¬КөРРөДКЗ·СВКёЎ¶Ҝ»ъЦЖЈ¬ЗТұЈ·СУлЙПТ»Дк¶ИіөБҫ·ўЙъөАВ·Ҫ»НЁКВ№КөДЗйҝцПаБӘПөЈ®·ўЙъҪ»НЁКВ№КөДҙОКэФҪ¶аЈ¬·СВКТІҫНФҪёЯЈ¬ҫЯМеёЎ¶ҜЗйҝцИзПВұнЈә
Ҫ»ЗҝПХёЎ¶ҜТтЛШәН·СВКёЎ¶ҜұИВКұн | ||
ёЎ¶ҜТтЛШ | ёЎ¶ҜұИВК | |
A1 | ЙПТ»ёцДк¶ИОҙ·ўЙъУРФрИОөАВ·Ҫ»НЁКВ№К | ПВёЎ10% |
A2 | ЙПБҪёцДк¶ИОҙ·ўЙъУРФрИОөАВ·Ҫ»НЁКВ№К | ПВёЎ20% |
A3 | ЙПИэёцј°ТФЙПДк¶ИОҙ·ўЙъУРФрИОөАВ·Ҫ»НЁКВ№К | ПВёЎ30% |
A4 | ЙПТ»ёцДк¶И·ўЙъТ»ҙОУРФрИОІ»Йжј°ЛАНцөДөАВ·Ҫ»НЁКВ№К | 0% |
A5 | ЙПТ»ёцДк¶И·ўЙъБҪҙОј°БҪҙОТФЙПУРФрИОөАВ·Ҫ»НЁКВ№К | ЙПёЎ10% |
A6 | ЙПТ»ёцДк¶И·ўЙъУРФрИОөАВ·Ҫ»НЁЛАНцКВ№К | ЙПёЎ30% |
Ді»ъ№№ОӘБЛСРҫҝДіТ»Ж·ЕЖЖХНЁ6ЧщТФПВЛҪјТіөөДН¶ұЈЗйҝцЈ¬Лж»ъійИЎБЛ60БҫіөБдТСВъИэДкёГЖ·ЕЖН¬РНәЕЛҪјТіөөДПВТ»ДкРшұЈКұөДЗйҝцЈ¬НіјЖөГөҪБЛПВГжөДұнёсЈә
АаРН | A1 | A2 | A3 | A4 | A5 | A6 |
КэБҝ | 10 | 5 | 5 | 20 | 15 | 5 |
(1)ЗуТ»БҫЖХНЁ6ЧщТФПВЛҪјТіөФЪөЪЛДДкРшұЈКұұЈ·СёЯУЪ»щұҫұЈ·СөДЖөВКЈ»
(2)Ді¶юКЦіөПъКЫЙМЧЁГЕПъКЫХвТ»Ж·ЕЖөД¶юКЦіөЈ¬ЗТҪ«ПВТ»ДкөДҪ»ЗҝПХұЈ·СёЯУЪ»щұҫұЈ·СөДіөБҫјЗОӘКВ№КіөЈ®јЩЙи№әҪшТ»БҫКВ№КіөҝчЛр5 000ФӘЈ¬Т»Бҫ·ЗКВ№КіөУҜАы10 000ФӘЈ®ЗТёчЦЦН¶ұЈАаРНөДЖөВКУлЙПКц»ъ№№өчІйөДЖөВКТ»ЦВЈ¬НкіЙПВБРОКМвЈә
ўЩИфёГПъКЫЙМөкДЪУР6Бҫ(іөБдТСВъИэДк)ёГЖ·ЕЖ¶юКЦіөЈ¬Ді№ЛҝНУыФЪөкДЪЛж»ъМфСЎ2БҫіөЈ¬ЗуХв2БҫіөЗЎәГУРТ»БҫОӘКВ№КіөөДёЕВКЈ»
ўЪИфёГПъКЫЙМТ»ҙО№әҪш120Бҫ(іөБдТСВъИэДк)ёГЖ·ЕЖ¶юКЦіөЈ¬ЗуТ»БҫіөУҜАыөДЖҪҫщЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝДіҝмІНҙъВфөкҙъКЫ¶аЦЦАаРНөДҝмІНЈ¬ЙоКЬ№гҙуПы·СХЯПІ°®.ЖдЦРЈ¬![]() ЦЦАаРНөДҝмІНГҝ·ЭҪшјЫОӘ
ЦЦАаРНөДҝмІНГҝ·ЭҪшјЫОӘ![]() ФӘЈ¬ІўТФГҝ·Э
ФӘЈ¬ІўТФГҝ·Э![]() ФӘөДјЫёсПъКЫ.Из№ыөұМм20:00Ц®З°ВфІ»НкЈ¬КЈУаөДёГЦЦҝмІНГҝ·ЭТФ
ФӘөДјЫёсПъКЫ.Из№ыөұМм20:00Ц®З°ВфІ»НкЈ¬КЈУаөДёГЦЦҝмІНГҝ·ЭТФ![]() ФӘөДјЫёсЧчМШјЫҙҰАнЈ¬ЗТИ«ІҝКЫНк.
ФӘөДјЫёсЧчМШјЫҙҰАнЈ¬ЗТИ«ІҝКЫНк.
ЈЁ1Ј©ИфёГҙъВфөкГҝМм¶ЁЦЖ![]() ·Э
·Э![]() ЦЦАаРНҝмІНЈ¬Зу
ЦЦАаРНҝмІНЈ¬Зу![]() ЦЦАаРНҝмІНөұМмөДАыИу
ЦЦАаРНҝмІНөұМмөДАыИу![]() ЈЁөҘО»ЈәФӘЈ©№ШУЪөұМмРиЗуБҝ
ЈЁөҘО»ЈәФӘЈ©№ШУЪөұМмРиЗуБҝ![]() ЈЁөҘО»Јә·ЭЈ¬
ЈЁөҘО»Јә·ЭЈ¬![]() Ј©өДәҜКэҪвОцКҪЈ»
Ј©өДәҜКэҪвОцКҪЈ»
ЈЁ2Ј©ёГҙъВфөкјЗВјБЛТ»ёцФВ![]() МмөД
МмөД![]() ЦЦАаРНҝмІНИХРиЗуБҝЈЁГҝМм20:00Ц®З°ПъКЫКэБҝЈ©
ЦЦАаРНҝмІНИХРиЗуБҝЈЁГҝМм20:00Ц®З°ПъКЫКэБҝЈ©
ИХРиЗуБҝ |
|
|
|
|
|
|
МмКэ |
|
|
|
|
|
|
ЈЁiЈ©јЩЙиҙъВфөкФЪХвТ»ёцФВДЪГҝМм¶ЁЦЖ![]() ·Э
·Э![]() ЦЦАаРНҝмІНЈ¬ЗуХвТ»ёцФВ
ЦЦАаРНҝмІНЈ¬ЗуХвТ»ёцФВ![]() ЦЦАаРНҝмІНөДИХАыИуЈЁөҘО»ЈәФӘЈ©өДЖҪҫщКэЈЁҫ«И·өҪ
ЦЦАаРНҝмІНөДИХАыИуЈЁөҘО»ЈәФӘЈ©өДЖҪҫщКэЈЁҫ«И·өҪ![]() Ј©Ј»
Ј©Ј»
ЈЁiiЈ©ИфҙъВфөкГҝМм¶ЁЦЖ![]() ·Э
·Э![]() ЦЦАаРНҝмІНЈ¬ТФ
ЦЦАаРНҝмІНЈ¬ТФ![]() МмјЗВјөДИХРиЗуБҝөДЖөВКЧчОӘИХРиЗуБҝ·ўЙъөДёЕВКЈ¬Зу
МмјЗВјөДИХРиЗуБҝөДЖөВКЧчОӘИХРиЗуБҝ·ўЙъөДёЕВКЈ¬Зу![]() ЦЦАаРНҝмІНөұМмөДАыИуІ»ЙЩУЪ
ЦЦАаРНҝмІНөұМмөДАыИуІ»ЙЩУЪ![]() ФӘөДёЕВК.
ФӘөДёЕВК.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝҪьДкАҙЈ¬ЦРГАГіТЧДҰІБІ»¶П.МШұрКЗГА№ъ¶ФОТ№ъ»ӘОӘөДПЮЦЖ.ҫЎ№ЬГА№ъ¶Ф»ӘОӘј«БҰ·вЛшЈ¬°Щ°гөуДСЈ¬ІўІ»¶ПјУҙу¶Фёч№ъөДК©С№Ј¬АӯВЈЛыГЗөЦЦЖ»ӘОӘ5GЈ¬И»¶шХвІўГ»УРИГ»ӘОӘИҙІҪ.»ӘОӘФЪ2018ДкІ»Ҫцҫ»АыИуҙҙПВјЗВјЈ¬әЈНвФціӨН¬СщЗҝҫў.ҪсДкЈ¬ОТ№ъ»ӘОӘДіТ»ЖуТөОӘБЛҪшТ»ІҪФцјУКРіЎҫәХщБҰЈ¬јЖ»®ФЪ2020ДкАыУГРВјјКхЙъІъДіҝоРВКЦ»ъ.НЁ№эКРіЎ·ЦОцЈ¬ЙъІъҙЛҝоКЦ»ъИ«ДкРиН¶Ил№М¶ЁіЙұҫ250НтЈ¬ГҝЙъІъ![]() ЈЁЗ§ІҝЈ©КЦ»ъЈ¬РиБнН¶ИліЙұҫ
ЈЁЗ§ІҝЈ©КЦ»ъЈ¬РиБнН¶ИліЙұҫ![]() НтФӘЈ¬ЗТ
НтФӘЈ¬ЗТ 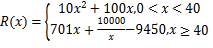 Ј¬УЙКРіЎөчСРЦӘЈ¬ГҝІҝКЦ»ъКЫјЫ0.7НтФӘЈ¬ЗТИ«ДкДЪЙъІъөДКЦ»ъөұДкДЬИ«ІҝПъКЫНк.
Ј¬УЙКРіЎөчСРЦӘЈ¬ГҝІҝКЦ»ъКЫјЫ0.7НтФӘЈ¬ЗТИ«ДкДЪЙъІъөДКЦ»ъөұДкДЬИ«ІҝПъКЫНк.
ЈЁ![]() Ј©Зуіц2020ДкөДАыИу
Ј©Зуіц2020ДкөДАыИу![]() ЈЁНтФӘЈ©№ШУЪДкІъБҝ
ЈЁНтФӘЈ©№ШУЪДкІъБҝ![]() ЈЁЗ§ІҝЈ©өДәҜКэ№ШПөКҪЈ¬ЈЁАыИу=ПъКЫ¶оЎӘіЙұҫЈ©Ј»
ЈЁЗ§ІҝЈ©өДәҜКэ№ШПөКҪЈ¬ЈЁАыИу=ПъКЫ¶оЎӘіЙұҫЈ©Ј»
![]() 2020ДкІъБҝОӘ¶аЙЩЈЁЗ§ІҝЈ©КұЈ¬ЖуТөЛщ»сАыИуЧоҙуЈҝЧоҙуАыИуКЗ¶аЙЩЈҝ
2020ДкІъБҝОӘ¶аЙЩЈЁЗ§ІҝЈ©КұЈ¬ЖуТөЛщ»сАыИуЧоҙуЈҝЧоҙуАыИуКЗ¶аЙЩЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘЦұПЯ![]() Ј®
Ј®
ЈЁ1Ј©ЗуЦӨЈәОЮВЫ![]() ИЎәОЦөЈ¬ЦұПЯ
ИЎәОЦөЈ¬ЦұПЯ![]() КјЦХҫӯ№эөЪТ»ПуПЮЈ»
КјЦХҫӯ№эөЪТ»ПуПЮЈ»
ЈЁ2Ј©ИфЦұПЯ![]() Ул
Ул![]() ЦбХэ°лЦбҪ»УЪ
ЦбХэ°лЦбҪ»УЪ![]() өгЈ¬Ул
өгЈ¬Ул![]() ЦбХэ°лЦбҪ»УЪ
ЦбХэ°лЦбҪ»УЪ![]() өгЈ¬
өгЈ¬![]() ОӘЧшұкФӯөгЈ¬Йи
ОӘЧшұкФӯөгЈ¬Йи![]() өДГж»эОӘ
өДГж»эОӘ![]() Ј¬Зу
Ј¬Зу![]() өДЧоРЎЦөј°ҙЛКұЦұПЯ
өДЧоРЎЦөј°ҙЛКұЦұПЯ![]() өД·ҪіМЈ®
өД·ҪіМЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘКэБР![]() өДЗ°
өДЗ°![]() ПоәНОӘ
ПоәНОӘ![]() Ј¬
Ј¬ ![]() Ј¬
Ј¬ ![]() Ј®өИ ІоКэБР
Ј®өИ ІоКэБР![]() ЦРЈ¬
ЦРЈ¬ ![]() Ј¬ЗТ№«Іо
Ј¬ЗТ№«Іо![]() Ј®
Ј®
ЈЁўсЈ©ЗуКэБР![]() өДНЁПКҪЈ»
өДНЁПКҪЈ»
ЈЁўтЈ©КЗ·сҙжФЪХэХыКэ![]() Ј¬К№өГ
Ј¬К№өГ![]() ?Ј®ИфҙжФЪЈ¬Зуіц
?Ј®ИфҙжФЪЈ¬Зуіц![]() өДЧоРЎЦөЈ»Иф І»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
өДЧоРЎЦөЈ»Иф І»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘФІ![]() Јә
Јә ![]() ҫӯ№эНЦФІ
ҫӯ№эНЦФІ![]() Јә
Јә ![]() өДЧуУТҪ№өг
өДЧуУТҪ№өг![]() Ј¬ЗТУлНЦФІ
Ј¬ЗТУлНЦФІ![]() ФЪөЪТ»ПуПЮөДҪ»өгОӘ
ФЪөЪТ»ПуПЮөДҪ»өгОӘ![]() Ј¬ЗТ
Ј¬ЗТ![]() Иэөг№ІПЯЈ¬ЦұПЯ
Иэөг№ІПЯЈ¬ЦұПЯ![]() Ҫ»НЦФІ
Ҫ»НЦФІ![]() УЪ
УЪ![]() Ј¬
Ј¬ ![]() БҪөгЈ¬ЗТ
БҪөгЈ¬ЗТ![]() ЈЁ
ЈЁ![]() Ј©.
Ј©.
ЈЁ1Ј©ЗуНЦФІ![]() өД·ҪіМЈ»
өД·ҪіМЈ»
ЈЁ2Ј©өұИэҪЗРО![]() өДГж»эИЎөГЧоҙуЦөКұЈ¬ЗуЦұПЯ
өДГж»эИЎөГЧоҙуЦөКұЈ¬ЗуЦұПЯ![]() өД·ҪіМ.
өД·ҪіМ.

Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ¶ЁТеФЪRЙПөДәҜКэfЈЁxЈ©Јҫ0Ј¬¶ФИОТвxЈ¬yЎКR¶јУРfЈЁx+yЈ©ЈҪfЈЁxЈ© fЈЁyЈ©іЙБўЈ¬ЗТөұxЈҫ0КұЈ¬fЈЁxЈ©Јҫ1Ј®
ЈЁ1Ј©ЗуfЈЁ0Ј©өДЦөЈ»
ЈЁ2Ј©ЗуЦӨfЈЁxЈ©ФЪRЙПКЗФцәҜКэЈ»
ЈЁ3Ј©ИфfЈЁk3xЈ©fЈЁ3x©Ғ9x©Ғ2Ј©Јј1¶ФИОТвxЎКRәгіЙБўЈ¬ЗуКөКэkөДИЎЦө·¶О§Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝСЎРЮ4-4ЈәЧшұкПөУлІОКэ·ҪіМ
ФЪЖҪГжЦұҪЗЧшұкПө![]() ЦРЈ¬ЗъПЯ
ЦРЈ¬ЗъПЯ![]() №эөг
№эөг![]() Ј¬ЖдІОКэ·ҪіМОӘ
Ј¬ЖдІОКэ·ҪіМОӘ ЈЁ
ЈЁ![]() ОӘІОКэЈ¬
ОӘІОКэЈ¬![]() Ј©Ј¬ТФ
Ј©Ј¬ТФ![]() ОӘј«өгЈ¬
ОӘј«өгЈ¬![]() Цб·Зёә°лЦбОӘј«ЦбҪЁБўј«ЧшұкПөЈ¬ЗъПЯ
Цб·Зёә°лЦбОӘј«ЦбҪЁБўј«ЧшұкПөЈ¬ЗъПЯ![]() өДј«Чшұк·ҪіМОӘ
өДј«Чшұк·ҪіМОӘ![]() .
.
ЈЁ1Ј©ЗуЗъПЯ![]() өДЖХНЁ·ҪіМәНЗъПЯ
өДЖХНЁ·ҪіМәНЗъПЯ![]() өДЦұҪЗЧшұк·ҪіМЈ»
өДЦұҪЗЧшұк·ҪіМЈ»
ЈЁ2Ј©ЗуТСЦӘЗъПЯ![]() әНЗъПЯ
әНЗъПЯ![]() Ҫ»УЪ
Ҫ»УЪ![]() Ј¬
Ј¬![]() БҪөгЈ¬ЗТ
БҪөгЈ¬ЗТ![]() Ј¬ЗуКөКэ
Ј¬ЗуКөКэ![]() өДЦө.
өДЦө.
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com