练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．设p：?x∈R，x2-4x+3m＞0，q：f（x）=x3+2x2+mx+1在（-∞，+∞）内单调递增，则p是q的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充分必要条件D．既不充分也不必要条件

    分析 函数单调递增等价于导函数大于等于0恒成立，故判别式小于等于0，求出命题p的等价条件，得到p，q的关系．从而得解．

    解答 解：∵p：?x∈R，x2-4x+3m＞0，
    ∴△=16-12m＜0，解得：m＞$\frac{4}{3}$，
    q：f（x）=x3+2x2+mx+1在（-∞，+∞）内单调递增，
    ∴f′（x）=3x2+4x+m≥0恒成立，
    ∴△=16-12m≤0，
    解得m≥$\frac{4}{3}$，
    ∴p是q的充分不必要条件，
    故选：A．

    点评 本题考查利用导数求函数的单调性及必要条件、充分条件、充要条件的判断．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

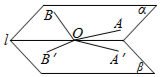    7．如图，小于90°的二面角α-l-β中O∈l，A，B∈α，且∠AOB为钝角，∠A′OB′是∠AOB在β内的射影，则下列结论一定错误的是（　　）
    A．∠A′OB′为钝角B．∠A′OB′＞∠AOB
    C．∠AOB+∠AOA′＜πD．∠B′OB+∠BOA+∠AOA′＞π

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    8．为普及学生安全逃生知识与安全防护能力，某学校高一年级举办了安全知识与安全逃生能力竞赛，该竞赛分为预赛和决赛两个阶段，预赛为笔试，决赛为技能比赛，现将所有参赛选手参加笔试的成绩（得分均为整数，满分为100分）进行统计，制成如下频率分布表．
    分数（分数段）频数（人数）频率
    [60，70）9x
    [70，80）y0.38
    [80，90）160.32
    [90，100）zs
    合计p1
    （1）求出上表中的x，y，z，s，p的值；
    （2）按规定，预赛成绩不低于90分的选手参加决赛．已知高一（2）班有甲、乙两名同学取得决赛资格，记高一（2）班在决赛中进入前三名的人数为X，求X的分布列和数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．当|x|≤1时，不等式2px2+qx-p+1≥0恒成立，求p+q的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    12．化简$\frac{sin（α+π）cos（π-α）sin（\frac{5}{2}π-α）}{tan（-α）co{s}^{2}（-α-2π）}$=-cosα．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知椭圆C：$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{33}}{7}$，且（4，0）在椭圆C上，圆M：x2+y2=65．
    （1）求椭圆C的方程；
    （2）已知A（m，n）为圆M上的任意一点，过点A作椭圆C的两条切线l1，l2，试探究直线l1，l2的位置关系，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知曲线E上的点M（x，y）到点F（2，0）的距离与到定直线x=$\frac{5}{2}$的距离之比为$\frac{2\sqrt{5}}{5}$．
    （I）求曲线E的轨迹方程；
    （Ⅱ）若点F关于原点的对称点为F′，则是否存在经过点F的直线l交曲线E于A、B两点，且三角形F′AB的面积为$\frac{40}{21}$，若存在，求出直线l的方程；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知点P是函数y=sin（2x+α）图象与x轴的一个交点，A，B为P点右侧距离点P最近的一个最高点和最低点，则$\overrightarrow{PA}$•$\overrightarrow{PB}$=（　　）
    A．$\frac{{π}^{2}}{4}$-1B．$\frac{3{π}^{2}}{16}$-1C．$\frac{3{π}^{2}}{4}$-1D．$\frac{{π}^{2}}{8}$-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．有一项活动，需在3名老师，8名男同学和5名女同学中选人参加．
    （1）若只需一人参加，有多少种不同方法？
    （2）若需老师、男同学、女同学各一人参加，有多少种不同选法？
    （3）若需一名老师，一名学生参加，有多少种不同选法？

    查看答案和解析>>

    同步练习册答案