已知函数f(x)=xk+b(常数k,b∈R)的图象过点(4,2)、(16,4)两点.
(1)求f(x)的解析式;
(2)记f(x)的反函数为g(x),解不等式g(x)+g(x-1)<2|x-2|;
(3)记f(x)的反函数为g(x),若不等式g(x)>ax-1恒成立,求实数a的取值范围.
【答案】
分析:(1)将(4,2)、(16,4)两点坐标代入函数f(x)=xk+b中,即可求出k、b的值,进而求得函数f(x)的解析式;
(2)根据前面求得的f(x)的解析式和题中已知条件可知函数g(x)的解析式,再解不等式
(3)不等式g(x)>ax-1恒成立等价于不等式x
2>ax-1在x∈[0,+∞)上恒成立,再进行分类讨论.
解答:解:(1)
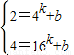
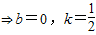
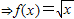
---------------(4分)
(2)g(x)=x
2(x≥0)---------------(6分)g(x)+g(x-1)<2|x-2|
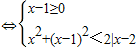
---------------(8分)
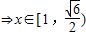
---------------(10分)
(3)g(x)=x
2(x≥0),不等式g(x)>ax-1恒成立等价于
不等式x
2>ax-1在x∈[0,+∞)上恒成立---------------(12分)
当x=0时,不等式x
2>ax-1恒成立;a∈R---------------(14分)
当x>0时,不等式
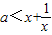
恒成立,
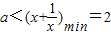
---------------(17分)
综上,实数a的取值范围为a∈(-∞,2)---------------(18分)
点评:本题主要考查了函数解析式的求法,函数的在区间上的恒成立问题常转化为求函数的最值,常用分离参数法.属于中档题

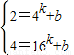
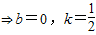
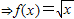 ---------------(4分)
---------------(4分)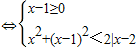 ---------------(8分)
---------------(8分)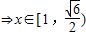 ---------------(10分)
---------------(10分)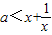 恒成立,
恒成立,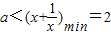 ---------------(17分)
---------------(17分)

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案 已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,|φ|<